5.1 Limitné [1] procesy a postupnosti
Väčšina činností, ktoré súvisia s meraním resp. určovaním nejakej hodnoty skúmanej veličiny má povahu procesu, ktorý by teoreticky mohol neobmedzene pokračovať, ale ktorý obvykle ukončujeme ak dosiahneme prijateľný výsledok. Prijateľným myslíme, že výsledok rešpektuje presnosť vyplývajúcu z kontextu úlohy. Príklady takýchto procesov sme už uviedli v predchádzajúcich kapitolách (pri skúmaní dĺžky uhlopriečky štvorca, pri približnom výpočte odmocnín, pri výpočte hodnoty $\pmb{ln \: 2}$). Ukážeme ďalšie príklady:
Príklad 1.
Častým limitným procesom je určovanie hmotnosti - váženie. Na obrázku vidíme váhy. Hmotnosť váženého telesa je $4.8282$ jednotiek [2], závažia majú hmotnosť $4.83$ jednotiek. Proces merania sme ukončili, pretože pridávaním menších závaží ako jedna stotina jednotky nedokážeme pozorovať zmenu výchylky ramien váh. Pokračovať v procese môžeme, ak zvýšime citlivosť váh. Môžeme to sledovať dynamicky v Cabri výkrese Váhy. Odvážte tam položené teleso s presnosťou na 10 desatiných miest. Keď skončíte, tak pomocou ikony "skry - ukáž" si odkryte skutočnú hmotnosť váženého telesa. Túto môžete meničom zmeniť a proces váženia opakovať.
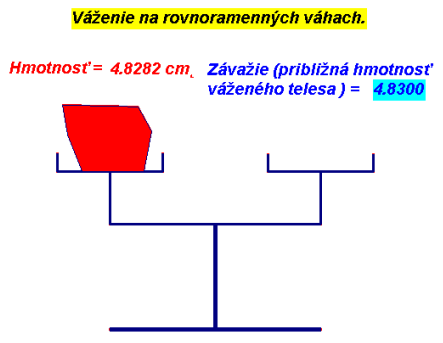
Váhy
Príklad 2.
Dôležitým "limitným procesom" je meranie dĺžky obvodu kružnice [3] . Ak sa pozriete na obrázok, na ktorom sú pravidelné n-uholníky vpísané do jednotkovej kružnice, iste vás napadne, že s rastúcim $\pmb{n}$ sa obvod týchto pravidelných n-uholníkov bude čím ďalej tým viac približovať k obvodu kružnice.

V Cabri výkrese Rektifikácia sme vypočítali a do tabuľky zapísali niektoré hodnoty $\pmb{O(n)}$. $$\begin{array} {|c|c|} \hline n & 3 & 4 & 5 & 6 & 7 & 30\\ \hline O(n) & 5.1962 & 5.6569 & 5.8779 & 6.0000 & 6.0744 & 6.2717\\ \hline \end{array}$$
Ako vidíte, tento spôsob približného určenia čísla $\bf{2\pi}$ (priame meranie dĺžky obvodu) nie je výhodný. Nie každý pravidelný n-uholník vieme zostrojiť (Cabri to dokáže cca do $n = 30$), meranie je nepresné a proces je „lenivý“, pomaly sa približuje k cieľu.
O niečo lepší spôsob by bol nájdenie nejakého rekurentného vzťahu medzi obvodmi vpísaných n-uholníkov. Pozrite si obrázok, pomocou ktorého vypočítame $\bf{O(2n)}$ pomocou $\bf{O(n)}$:
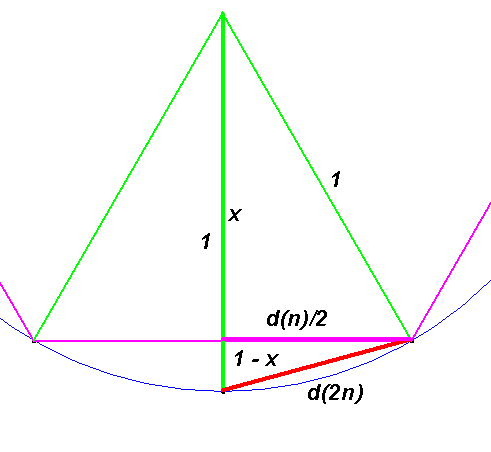
Zrejme platia vzťahy: $$\bf{x = \sqrt{1-\frac{d^2_n}{4}} \qquad d_{2n} = \sqrt{(1-x)^2 + \frac{d^2_n}{4}}} \qquad (^4)$$ Z týchto vzťahov po úprave dostávame: $$\bf{d_{2n} = \sqrt{2-\sqrt{4-d_n^2}}}$$
Proces môžeme začať od pravidelného šesťuholníka, pretože vieme, že $\bf{d_6 = 1}$.
Na postupný výpočet obvodov vpísaných n-uholníkov sme použili EXCEL (otvorte si zošit Rektifikácia). Proces sme ukončili po dvanástich krokoch. Potom začína byť problém s tým, že násobíme príliš malé číslo $\bf{d_n}$ príliš veľkým číslom $\bf{n}$, čo spôsobuje nepresnosti. Pre porovnanie sme uviedli aj približnú hodnotu čísla $\bf{2\pi}$.