5.3 Plošné obsahy
V 5. príklade kapitoly 4.1 sme neodpovedali na otázku, ktorá časť obdĺžnikovej záhrady na obrázku vľavo je väčšia. Tá, z ktorej je bližšie ku studni (t.j. k bodu $\pmb{F}$), alebo tá, z ktorej je bližšie k potoku (t.j. k priamke $\pmb{d}$)?
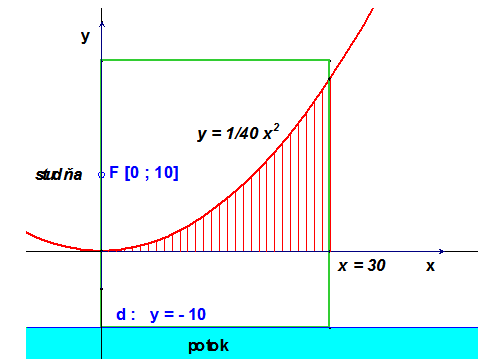
Stačí ak budeme vedieť vypočítať obsah vyšrafovaného plošného útvaru, ktorý je ohraničený grafom funkcie $\pmb{y = 0.025 \cdot x^2}$, priamkou $\pmb{x = 30}$ a osou $\pmb{x}$.
Vo všeobecnosti, chceme zistiť, ako sa dá vypočítať obsah plošného útvaru ohraničeného osou x, grafom funkcie [1] $y = f(x)$ a priamkami $x = a, x = b$.
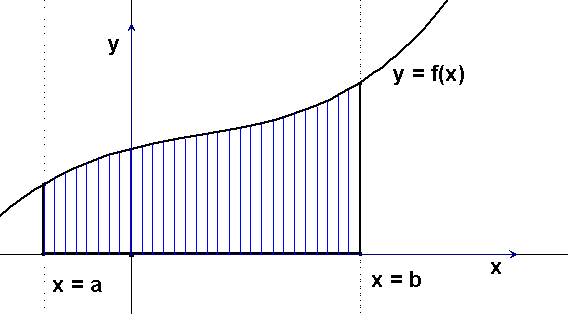
Veľkosť obsahu vyšrafovaného útvaru sa volá určitý integrál z funkcie $f(x)$ od $a$ do $b$ a označuje sa symbolom: $$\bbox[yellow, 5px]{\pmb{\int_a^b f(x)dx}}$$
Príklad 1.
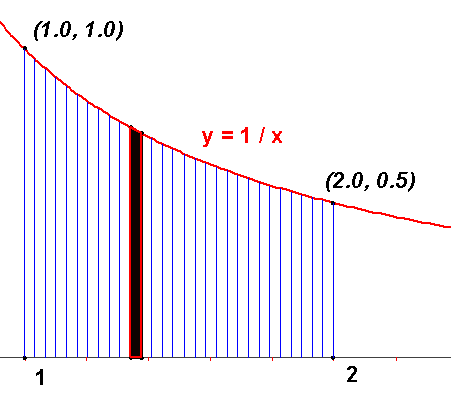
Spomínate si na Príklad 3. z kapitoly IV.2? Tam sme počítali obsah oblasti ohraničenej grafom funkcie $\pmb{y = \frac{1}{x}}$ s osou $\pmb{x}$ a priamkami $\pmb{x = 1}$ a $\pmb{x = 2}$.
Približnú hodnotu obsahu vyšrafovanej oblasti $\pmb{P(n)}$ sme získali ako súčet obsahov $\pmb{n}$ vpísaných lichobežníkov s rovnakou výškou $\pmb{\frac{1}{n}}$.
Pritom $\pmb{P(1) = 0.75}$ a platil rekurentný vzťah:
Tento vzťah sme zužitkovali pri výpočte v 2. hárku zošitu ln(2). Vypočítali sme $\bf{P(n)}$ pre $\bf{n}$ od $\bf{1}$ do $\bf{2000}$. Získali sme približnú hodnotu $\bf{P(2000) = 0,6931471962}$, čo je približne prirodzený logaritmus z čísla 2.