5.2 Dotyčnice
Príklad 1.
Ako vieme už od čias Galileiho [ 1], ak pustíme kameň z výšky $20$ metrov (a zanedbáme odpor vzduchu), jeho výška $\pmb{h(t)}$ (metrov) v čase $\pmb{t}$ sekúnd bude približne: $\pmb{h(t) = 20 - 4.9 \cdot t^2}$.
Aká bude jeho rýchlosť v čase $\pmb{t = 1}$ (sekunda)?
Budeme merať priemernú rýchlosť v intervale $\pmb{(1; 1 + \Delta t)}$, pričom hodnotu $\pmb{\Delta t}$ budeme postupne zmenšovať vždy na desatinu pôvodnej hodnoty: $$\begin{array} {|c|c|} \hline \Delta t & h(1 - \Delta t) & h(1) & h(1 + \Delta t) & \frac{h(1 + \Delta t) - h(1)}{\Delta t} & \frac{h(1 + \Delta t) - h(1 - \Delta t)}{2 \Delta t} \\ \hline 0.1 & 16.031 & 15.1 & 14.071 & -10.29 & -9.8\\ \hline 0.01 & 15.19751 & 15.1 & 15.00151 & -9.849 & -9.8\\ \hline 0.001 & 15.1097951 & 15.1 & 15.0901951 & -9.8049 & -9.8\\ \hline 0.0001 & 15.10097995 & 15.1 & 15.09901995 & -9.80049 & -9.8\\ \hline 0.00001 & 15.100098 & 15.1 & 15.099902 & -9.800049 & -9.8\\ \hline 0.000001 & 15.1000098 & 15.1 & 15.0999902 & -9.8000049 & -9.8\\ \hline \end{array}$$
V 5. stĺpci tabuľky (zhotovili sme ju v 1. hárku zošitu fluxie) vidíme, že priemerná rýchlosť sa postupne približuje k hodnote $\pmb{-9.8}$.
Ak by sme merali priemernú rýchlosť v intervale $\pmb{(1 - \Delta t; 1 + \Delta t)}$, bola by bez ohľadu na voľbu $\pmb{\Delta}$ vždy $\pmb{-9.8}$ (metra za sekundu). Preto môžeme povedať, že okamžitá rýchlosť telesa padajúceho voľným pádom je v čase $\pmb{1 \: s}$ približne rovná hodnote $\pmb{-9.8[m/s]}$.
Príklad 2.
Zostrojme dotyčnicu ku grafu funkcie $\pmb{f(x) = 20 - 4.9 \cdot x^2 }$ v bode $\pmb{1; 15.1}$.
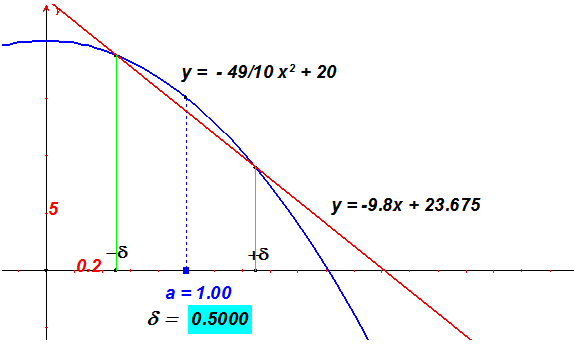
Problémom je samotný pojem dotyčnice ku grafu funkcie (alebo k nejakej krivke). Vieme zostrojiť dotyčnicu ku kružnici, v knihe Geometria sa naučíme zostrojovať dotyčnice k niektorým ďalším krivkám, ale algoritmus na zostrojenie dotyčnice (napríklad pomocou pravítka a kružidla) k ľubovoľnej krivke neexistuje. Môžeme však postupne zostrojovať sečnice grafu spájajúce dva jeho body, pričom tieto body budú po každom kroku k sebe bližšie. Tento limitný proces po konečnom počte krokov vedie k zostrojeniu takej sečnice grafu, ktorá sa od kýženej dotyčnice síce líši, ale len o toľko, akú presnosť sme si zvolili.
Proces vo svojej dynamike môžeme sledovať v Cabri výkrese Dotyčnica.