2. Riešenia úloh
Úlohy z kapitoly 2.1
-
Podľa výsledku zo 4. príkladu: $$P(\alpha) = \bbox[yellow, 5px]{\pmb{\pi \frac{(sin\alpha + 1)^2}{sin\alpha cos^2\alpha}}}$$ a z faktu, že $$\pmb{x = \frac{r}{s} = sin\alpha} \text{,}$$ dostávame: $$\pmb{P(x) = \pi \frac{(x + 1)^2}{x(1 - x^2)} = \pi \frac{x + 1}{x(1 - x)}, x \in (0; 1)}$$
Pozrite si graf v GO5d.
-
Z výkresu Pokrytie pologule vyplýva, že pre povrch plášťa $\pmb{P}$ platí: $\pmb{P = \pi \cdot r \cdot s}$.
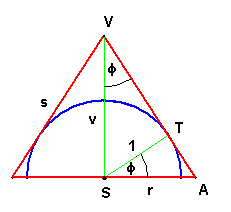
Z podobnosti trojuholníkov $\pmb{ASV}$ a $\pmb{ATS}$ dostávame $\pmb{\frac{r}{s} = \frac{\sqrt{r^2 - 1}}{r}}$. Preto: $\bbox[yellow, 5px]{\pmb{P(r) = \frac{\pi r^3}{\sqrt{r^2 - 1}}}}$, $\pmb{r > 1}$. Ak použijeme ako premennú výšku $\pmb{v}$, dvojaké vyjadrenie obsahu trojuholníka $ASV$ dáva: $\pmb{s \cdot 1 = v \cdot r}$ a Pytagoras: $\pmb{s^2 = r^2 + v^2}$ odtiaľ dostávame $\pmb{r = \frac{v}{\sqrt{v^2 - 1}}, s = \frac{v^2}{\sqrt{v^2 - 1}}}$ a preto $\bbox[yellow, 5px]{\pmb{P(v) = \frac{\pi v^3}{v^2 - 1}}}, \pmb{v > 1}$. Pozrite si G06a a G06b.
G06a
G06b
Vyjadrenie povrchu plášťa pomocou veľkosti uhla $\varphi$, ktorý zvierajú povrchové priamky kužeľa s jeho osou nájdete v 3. príklade kapitoly 5.4.
-
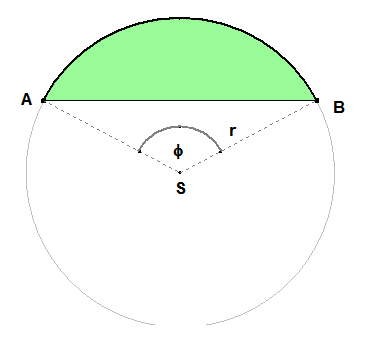
Je zrejmé, že $\bf{r \cdot \varphi = 10}$. Ak označíme obsah odseku ako $\bf{O}$, obsah kruhového výseku so stredovým uhlom $\varphi$ ako $\bf{V}$ a obsah trojuholníka $\bf{ABS}$ ako $\bf{T}$ zrejme platí: $$\bf{ V = \pi r^2 \frac{\varphi}{2\pi} = \frac{r^2 \varphi}{2}, \\ T = \frac{r^2 \sin \varphi}{2}, \\ O = V - T, \\ O = \frac{r^2}{2}(\varphi - \sin \varphi) }$$
Ak použijeme ako premennú $\bf{r}$ máme: $$\bf{\bbox[yellow, 5px]{O = \frac{r^2}{2} \Biggl ( \frac{10}{r} - \sin \biggl ( \frac{10}{r} \biggr ) \Biggr )} \, , r \geq \frac{5}{\pi}}$$
Vyjadrenie obsahu odseku nad tetivou $AB$ pomocou veľkosti stredového uhla nájdete v 4. príklade kapitoly 5.4.
Pozrite si tiež G07.
-
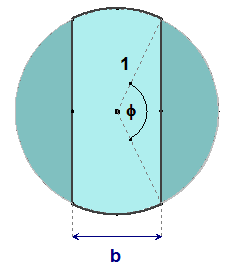
Ak využijeme vyjadrenie pre veľkosť odseku z riešenia predchádzajúcej úlohy a zohľadníme, že $\bf{r = 1}$, tak pre zvyšok $\bf{Z(\varphi)}$ platí: $$\bf{\bbox[yellow] {Z(\varphi) = \pi - \varphi + \sin \varphi,} 0 \lt \bbox[yellow, 5px] \varphi \lt \bbox[yellow, 5px] \pi }$$
Z faktu $\bf{b / 2 = \cos(\varphi / 2)}$ vyplýva $\bf{\varphi = 2 \arccos(b/2)}$. Odtiaľ máme trochu kostrbaté vyjadrenie: $$\bf{\bbox[yellow]{Z(b) = \pi - 2\arccos(b/2) + \sin(2\arccos(b/2))},}$$ kde $\bf{0 \lt b \lt 2}$. Pozrite si G08a a G08b.
G08a
G08b