2.1 Premenná
Jazyk matematiky [1] sa vyvíja a etapy jeho vývoja sú aj etapami vývoja matematiky [2]. Cesta viedla od primitívneho záznamu nejakého množstva najprv pomocou vrypov, alebo kôpok kamienkov, až po zápis čísla pomocou číslic v pozičnej číselnej sústave, cez jazyk receptov na výpočet plôch a objemov v Mezopotámii a v Egypte, cez starogrécky jazyk geometrie, čiže zostrojovanie úsečiek, ktorých dĺžka je závislá od dĺžok daných úsečiek, cez prvé pokusy označovať neznámu veličinu písmenom r (od prvého písmena latinského slova res - po slovensky vec), až po Viétovu [ 3] ideu používať písmená aj pre označovanie ľubovoľných čísel. To posledné oddelilo aritmetiku (narábanie s číslami) od algebry (narábanie so symbolmi).
Označovanie neznámej (premennej) veličiny písmenom a Descartesov objav používať čísla (respektíve dvojice či trojice čísel) na určovanie polohy, rozviazali matematikom ruky pri vyjadrovaní vzťahov a závislostí medzi veličinami reálneho sveta. Dôležitosť tohto faktu trvá aj dnes v dobe rozvoja najrôznejších technológií. Počítač s pomocou vhodného softvéru je účinný nástroj pri riešení rovníc, vie znázorniť priebeh ľubovoľnej závislosti (dvoch alebo i viacero) veličín, ale objaviť túto závisloť, vyjadriť hľadaný vzťah medzi veličinami ako nejakú funkciu, zostaviť rovnicu, ktorú treba vyriešiť, to dokáže (i keď mnohokrát tiež s pomocou počítačov) len človek.
V nasledujúcich príkladoch a úlohách vás chceme presvedčiť, že schopnosť vyjadriť hľadanú závislosť, schopnosť vhodne si zvoliť premennú, patrí v dobe informačných a komunikačných technológií medzi najdôležitejšie kompetencie (matematicky) vzdelaného človeka.
Príklad 1.
Na obrázku vidíme obdĺžnik $\bf{ABCD}$ s rozmermi $\bf{AB = a}$, $\bf{AD = b}$ a úsečku $\bf{XY}$, ktorá prechádza bodom $\bf{C}$ a jej koncové body ležia na polpriamkach $\bf{AB}$ a $\bf{AD}$. Vyjadrite dĺžku úsečky $\bf{XY}$.
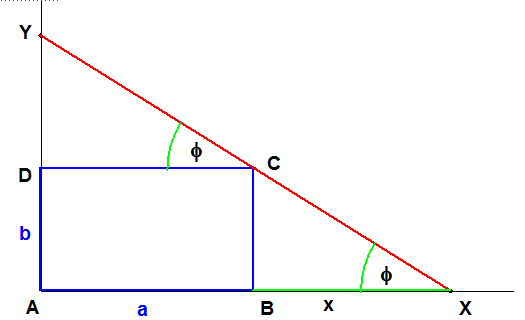
Ako vhodné premenné na vyjadrenie dĺžky úsečky $\bf{XY}$ sa núkajú:
- Dĺžka ${x}$ úsečky $\bf{BX}$
- Veľkosť $\bf{\varphi}$ uhla $\bf{AXY}$
V 1. prípade ak označíme ${|DY| = y}$, tak z podobnosti trojuholníkov $BXC$ a $DCY$ dostávame: $$\bf{\frac{y}{a} = \frac{b}{x} \Rightarrow y = \frac{ab}{x}}$$ a odtiaľ $$\bf{|XY| = |XC| + |CY| = \bbox[yellow, 5px]{\sqrt{x^2 + b^2} + \sqrt{\biggl( \frac{ab}{x} \biggr )^2 + a^2}}}$$
V 2. prípade máme $\bf{\frac{b}{|XC|} = \sin\varphi, \frac{a}{|CY|} = \cos\varphi}$ a z toho dostávame: $$\bbox[aqua, 5px]{\bf{|XY| = \frac{a}{\cos\varphi} + \frac{b}{\sin\varphi} }}$$
Treba poznamenať, že v 1. prípade je $x$ ľubovoľné kladné číslo a v 2. prípade je uhol $\bf{AXY}$ vždy ostrý, čiže $\bf{\varphi \in (0; \frac{\pi}{2})}$.
Nájdené vyjadrenia sa dosť líšia. Odpovedať na otázku, ktoré je vhodnejšie, má zmysel až potom, keď budeme vedieť na čo tieto vyjadrenia použijeme.
Príklad 2.
Vyjadrite obsah pravouholníka $\bf{ABCD}$ s obvodom $\bf{4d}$ pomocou:
- dĺžky $\bf{x}$ dlhšej strany
- pomeru $\bf{k}$ dĺžok jeho strán
- dĺžky $\bf{u}$ jeho uhlopriečky
- rozdielu $\bf{\Delta}$ dĺžok jeho strán
Prípad a. je zrejmý (pozri Obsah a), obsah $\bf{P(x) = \bbox[yellow, 5px]{x \cdot (2d - x)},
x \in \langle d ; 2d )}$.
Obsah a
V prípade b. (pozri Obsah b) dostávame $\bf{a + k \cdot a = 2d}$, odkiaľ máme:
Obsah b
G04
Zaujímavý je prípad c. Nebudeme sa tu púšťať do riešenia úlohy ako zostrojiť obdĺžnik, keď poznáme jeho
obvod a dĺžku uhlopriečky (ale zamyslenie sa nad výkresom Obsah c môže byť poučné). Stačí, keď si uvedomíme, že:
$$\bf{u^2 = a^2 + b^2, \, 2d = a + b \Rightarrow}$$
$$\bf{4d^2 = a^2 + 2ab + b^2 = u^2 + 2 \cdot P(u) \Rightarrow}$$
$$\bf{P(u) = \bbox[yellow, 5px]{2d^2 - \frac{u^2}{2}}}.$$
Obsah c
Musíme si uvedomiť, že $\bf{u \in \langle \sqrt{2} \cdot d; 2d)}$.
Pre riešenie prípadu d. nepotrebujeme ilustráciu. Zo sústavy rovníc: $$\bf{a - b = \Delta, \, a + b = 2d}$$ dostávame $$\bf{a = d + \frac{\Delta}{2}, \, b = d - \frac{\Delta}{2}},$$ takže pre obsah dostávame vzťah: $$\bf{P(\Delta) = \bbox[yellow, 5px]{d^2 - \frac{\Delta^2}{4}}, \Delta \in \langle 0; 2d )}$$
Odpovedať na otázku, ktorá z volieb premennej bola najvhodnejšia, má zmysel len ak vieme čo sme chceli takýmto vyjadrením obsahu dosiahnuť. Prípad d. je napríklad najvhodnejší pri riešení problému, kedy je obsah maximálny.