1.3 Diery v číselnej osi alebo iracionálne čísla
Príklad 1.
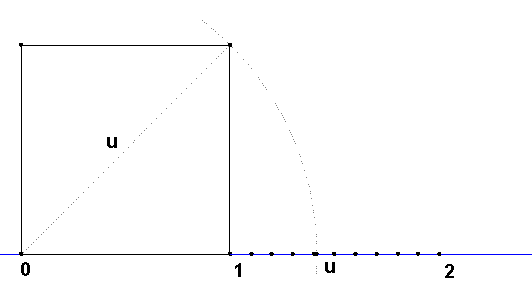
Zostrojme na číselnej osi bod u, ktorý má od začiatku vzdialenosť rovnú dĺžke uhlopriečky štvorca, ktorého strana má dĺžku 1.
Otázka znie, je to obraz niektorého racionálneho čísla?
Vďaka Pytagorovej vete vieme, že $\bf{u^2 = 2}$. Preto číslo $\bf{u}$ leží medzi číslami $\bf{1}$ a $\bf{2}$. Keby sme sa pozreli z bližšia (pozrite si 1. list zošitu UHLOPRIEČKA), dostávali by sme pre číslo $\bf{u}$ (teda pre dĺžku skúmanej uhlopriečky štvorca s jednotkovou stranou) postupne tieto ohraničenia: $$\bf{1.4 \lt u \lt 1.5}$$ $$\bf{1.41 \lt u \lt 1.42}$$ $$\bf{1.414 \lt u \lt 1.415}$$
UHLOPRIEČKA
V praxi s meraním obvykle končíme, keď dosiahneme požadovanú presnosť, respektíve, keď nám používané náčinie neumožňuje pokračovať. Experimentovanie v Exceli(jeho možnosti sú ohraničené presnosťou reprezentácie reálnych čísel v pamäti počítača) sme skončili pri čísle $\bf{1.414213562373}$.
Vzniká vážne podozrenie, že keby sme pokračovali ľubovoľne dlho, nikdy by sme nezískali desatinné číslo, ktorého druhá mocnina sa rovná dvom. Žiaľ, toto podozrenie sa pokračovaním vo výpočte nedá dokázať (je totiž možné, že po ďalšom výpočte by sa začali cifry periodicky opakovať).
Týmto problémom sa zaoberali grécki matematici, súčasníci Pytagora. Oni riešili problém:
"Existuje štvorec
[1]
, ktorý je súčtom dvoch rovnakých štvorcov?"
V našej terminológii: Existujú také prirodzené čísla $\bf{a, b}$, že $\bf{a^2 = b^2 + b^2}$ ? (*)
Uvažovali asi takto. Nech také dvojice prirodzených čísel, ktoré spĺňajú vzťah (*) existujú. Potom je jedna z nich, napríklad $\bf{m, n}$ iste najmenšia. Teda $\bf{m^2 = n^2 + n^2}$.
Uvažujme čísla $\bf{p = m - n, q = 2n - m}$. Ukážeme, že tiež spĺňajú vzťah (*). Naozaj, $$\bf{q^2 = (2n - m)^2 = 4n^2 - 4nm + m^2 = 4n^2 - 4nm + 2n^2 = 6n^2 - 4mn}$$ $$\bf{2 \cdot p^2 = 2(m - n)^2 = 2m^2 - 4mn + 2n^2 = 6n^2 - 4mn}$$ Ale dvojica $\bf{p, q}$ je už menšia ako dvojica $\bf{m, n (p + q = n)}$, preto predpoklad, že existujú také dvojice prirodzených čísel, ktoré spĺňajú vzťah (*) je falošný, vedie ku sporu.
Tvrdenie (*) je ekvivalentné s tvrdením, že existuje také racionálne číslo $\bf{u}$, pre ktoré platí: $$\bf{u^2 = 2}$$
- lebo
Týmto spôsobom sme zistili, že ten bod číselnej osi, ktorého vzdialenosť od začiatku je rovná dĺžke uhlopriečky jednotkového štvorca, nie je obrazom žiadneho racionálneho čísla, alebo inak povedané "racionálna" číselná os má "diery". Takých "dier" v racionálnej číselnej osi je nespočetne mnoho. Napríklad neexistujú také racionálne čísla, ktorých druhá mocnina $\bf{3}$, alebo $\bf{5, 6, 7, 8, 10,}$ ...