MATEMATICKÁ ČÍTANKA

Pri výpočte hodnoty tzv. racionálnej funkcie ^[2] získame výsledok po vykonaní konečného počtu sčítaní, odčítaní, násobení a delení. Horšie je to s ostatnými funkciami. Napríklad ľubovoľná odmocnina. Číslo $\pmb{b = \sqrt[q]{a}(q \in N, a \geq 0)}$ je definované ako "také nezáporné číslo, ktorého q-ta mocnina je rovná číslu a". V tejto definícii nie je ani náznak algoritmu, ktorý by po vykonaní konečného počtu základných operácii viedol k výpočtu odmocniny. Takto "nekonštruktívne", t.j. nie návodom na výpočet, ale popisom vlastností je v matematike definovaných množstvo objektov.

Za onoho času, keď ešte neexistovali počítače, vznikali problémy ako ľahko a rýchle vypočítať rôzne odmocniny a iné veličiny, ktoré boli definované nekonštruktívne.

Matematici si uvedomovali súvislosť medzi takýmito dvoma radmi čísel: \begin{array}{:c:c:c|c|c:c|c|c:c:c|c|c:}\hdashline \cellcolor{yellow}1 & \cellcolor{yellow}2 & \cellcolor{yellow}3 & \cellcolor{yellow}\bf{4} & \cellcolor{yellow}5 & \cellcolor{yellow}6 & \cellcolor{yellow}\bf{7} & \cellcolor{yellow}8 & \cellcolor{yellow}9 & \cellcolor{yellow}10 & \cellcolor{yellow}\bf{11} & \cellcolor{yellow}12 \\ \hdashline \cellcolor{#AFF}2 & \cellcolor{#AFF}4 & \cellcolor{#AFF}8 & \cellcolor{#AFF}\bf{16} & 3\cellcolor{#AFF}2 & \cellcolor{#AFF}64 & \cellcolor{#AFF}\bf{128} & \cellcolor{#AFF}256 & \cellcolor{#AFF}512 & \cellcolor{#AFF}1024 & \cellcolor{#AFF}\bf{2048} & \cellcolor{#AFF}4096 \\ \hdashline \end{array}

Pre orámované žlté čísla platí, že tretie je súčtom prvých dvoch ale pre orámované modré čísla platí, že tretie je súčinom prvých dvoch.

Súvislosť medzi horným (aritmetickým) a dolným (geometrickým) radom udáva takzvaná "exponenciálna" funkcia: $$\pmb{y = a^x, a \in R^+ \land a \neq 1}$$

Táto súvislosť by sa dala využiť. Keby sme dobre poznali graf jednej exponenciálnej funkcie $\pmb{y = a^x}$, mohli by sme násobenie nahradiť sčitovaním. Ak by sme mali vynásobiť dve čísla $\pmb{u}$ a $\pmb{v}$, stačilo by nájsť ich obrazy na osi y, pomocou grafu nájsť ich vzory $\pmb{k, l}$ na osi x, tieto sčítať a opäť pomocou grafu nájsť obraz $\pmb{u \cdot v}$ súčtu $\pmb{k + l}$. Dobre to vidíme na obrázku:

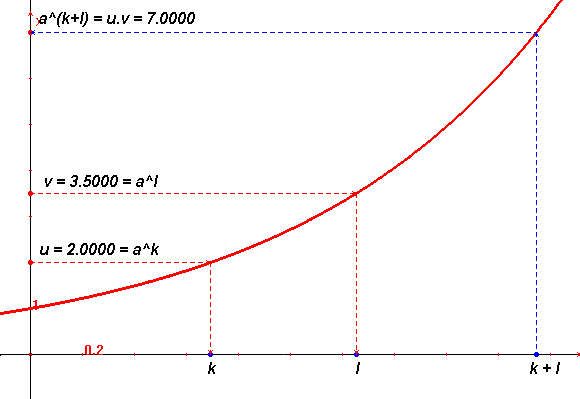
V "živej" podobe, v ktorej si môžete čísla $\pmb{u, v}$ ľubovoľne meniť si to môžete pozrieť na výkrese Exp01.

Ešte väčšou výhodou by bola možnosť nahradiť pomocou grafu exponenciálnej funkcie umocňovanie násobením, resp. odmocňovanie delením. Ak by sme mali umocniť číslo $\bf{u}$ exponentom $\bf{p}$, stačilo by nájsť obraz čísla $\bf{u}$ na osi $y$, pomocou grafu nájsť jeho vzor $\bf{k}$ na osi $x$, tento vynásobiť číslom $\bf{p}$ a opäť pomocou grafu nájsť jeho obraz $\bf{u^p}$ na osi $y$. Lepšie to vidíme na obrázku:

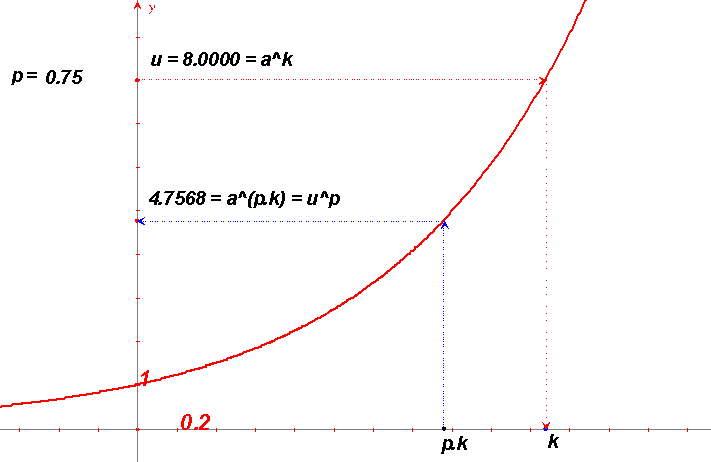
V „živej“ podobe, v ktorej môžete čísla $\bf{u, p}$ ľubovoľne meniť si to môžete pozrieť na výkrese Exp02.

Problém je v slovách „keby sme poznali“. Čo to vlastne znamená dobre poznať nejakú funkciu $\bf{y = f(x)}$? Slová „pomocou grafu nájsť jeho vzor $\bf{k}$ na osi $x$“ a „opäť pomocou grafu nájsť jeho obraz $\bf{u^p}$ na osi $y$“ predpokladajú že vieme bezprostredne k ľubovoľnému $\bf{x}$ určiť príslušné $\bf{y}$ a aj naopak, k ľubovoľnému $\bf{y}$ určiť príslušné $\bf{x}$. Pre exponenciálnu funkciu so základom $\bf{a}$ to znamená, že vieme vypočítať aj také hodnoty ako napr. $\bf{a^{0.123}}$.

Zdá sa, že sme sa ocitli v bludnom kruhu. Chceme dobre spoznať jednu exponenciálnu funkciu (napríklad radi by sme ju mali „tabelovanú“), aby sme si uľahčili napr. výpočet zložitých mocnín, ale k tomu potrebujeme vedieť vypočítať práve takéto zložité mocniny. Ono to vlastne nie je bludný kruh. Stačí nám nájsť jeden taký základ a, ktorého mocniny dokážeme vypočítať, tým získame exponenciálnu funkciu a pomocou nej už budeme môcť počítať mocniny s ľubovoľným základom.

Sformulujme náš problém:

Hľadá sa také $\bf{a}$, pre ktoré vieme vypočítať napr. $\bf{a^{0.123}}$. Uvedomme si, že: $$\bf{a^{0.123} = a^{\frac{123}{1000}} = \sqrt[1000]{a^{123}} = (\sqrt[1000]{a})^{123} }$$

Pri výrobe tabuliek funkcie $\bf{y = a^x}$ bude najvhodnejší posledný tvar. Takže stačí nájsť také $\bf{a}$, z ktorého vieme vypočítať tisícu odmocninu. Také $\bf{a}$ však poznáme, stačí zvoliť $\bf{a = b^{1000}}$.

Problém sme redukovali na nájdenie vhodného čísla $\bf{b}$. Aké požiadavky má spĺňať?

• číslo $\bf{b}$ má mať vhodnú veľkosť. Zrejme má byť $\bf{b \lt 0}$. Ohraničenie zhora je dané tým, že vyžadujeme, aby tabuľky boli približne rovnako „husté“ na osi x ako aj na osi y. Inak povedané, vieme že interval $\bf{\langle 0; 1 \rangle}$ sa zobrazí do intervalu $\langle 1; a \rangle$ a my chceme aby tieto intervaly boli približne rovnako veľké. To znamená, že chceme, aby $\bf{a - 1}$ čiže $\bf{b^{1000}-1}$ bolo rádovo jednotka.

• Ak budeme robiť tabuľky od nuly, s krokom napr. $\bf{0.001}$, budeme postupne počítať hodnoty $\bf{a^0 = b^0, \; a^{0.001} = b^1,\; a^{0.002} = b^2}$ atď. To znamená každú ďalšiu hodnotu dostaneme z predchádzajúcej prenásobením číslom $\bf{b}$. Vieme že písomné násobenie je zdĺhavé (pozor, rozprávka je z čias, keď nepoznali ani počítače, ani kalkulačky !), preto číslo $\bf{b}$ by malo obsahovať také cifry, aby sa ním ľahko násobilo. Také cifry sú nuly a jednotky. Poďme hľadať vhodný základ:

  (pozri e02)

  
  
  \begin{array}{:c:c:}\hdashline \bf{b} & \bf{b^{1000}} & \bf{b^{10000}} & \bf{b^{100000}} & \bf{b^{100000}}\\ \hdashline 1,1000000 & \text{Príliš veľké} & \text{Príliš veľké} & \text{Príliš veľké} & \text{Príliš veľké}\\ \hdashline 1,0100000 & 20959,1556378 & \text{Príliš veľké} & \text{Príliš veľké} & \text{Príliš veľké}\\ \hdashline 1,0010000 & \cellcolor{cyan}2,7169239 & 21916,6813390 & \text{Príliš veľké} & \text{Príliš veľké} \\ \hdashline 1,0001000 & 1,1051654 & \cellcolor{cyan}2,7181459 & 22015,4560485 & \text{Príliš veľké} \\ \hdashline 1,0000100 & 1,0100501 & 1,1051704 & \cellcolor{cyan}2,7182682& 22025,3645083 \\ \hdashline 1,0000010 & 1,0010005 & 1,0100502 & 1,1051709 &\cellcolor{cyan} 2,7182805 \\ \hdashline \end{array}

  Pri kroku $\bf{0,001}$ bude vhodný základ $\bf{a = 1,001^{1000} = 2,716923932}$

  Pri kroku $\bf{0,0001}$ bude vhodný základ $\bf{a = 1,0001^{10000} = 2,718145927}$

  Pri kroku $\bf{0,00001}$ bude vhodný základ $\bf{a = 1,00001^{100000} = 2,718268237}$

  Pri kroku $\bf{0,000001}$ bude vhodný základ $\bf{a = 1,000001^{1000000} = 2,718280469}$

čiže pri kroku $\bf{10^{– n}}$ bude vhodný základ: $$\bf{a_n = (1 + 10^{(-10)})^{(10^n)} }$$