1.2. Racionálne čísla
Prirodzené čísla vznikli abstrakciou procesu spočítavania konečných skupín objektov. No v bežnom živote nielen spočitjeme množstvá individuálnych objektov, ale aj meriame veličiny, ako sú napríklad dĺžka, obsah, objem, uhol, hmotnosť, čas, ... . Ak chceme zaručiť možnosť spracovávať, porovnávať, vyhodnocovať alebo inak využívať výsledky týchto meraní, musíme rozšíriť "obzory aritmetiky" aj o číselné vyjadrenie miery najrôznejších veličín.
Pri meraní veličín tieto obvykle porovnávame s nejakou (ľubovoľne) zvolenou jednotkou [1] . (V histórii existovalo a ešte aj dnes existuje veľké množstvo jednotiek pre všetky druhy veličín i keď "normalizácia" v technike a vo vedách sa snaží v systéme jednotiek zabezpečiť poriadok.)
Máloktorá meraná veličina je zhodná priamo so zvolenou jednotkou, alebo jej násobkom. Na obrázku porovnávame čiernu úsečku s dvojyardovou tyčou. Naša úsečka je dlhšia ako $1$ yard, ale kratšia ako dva yardy. Preto nasleduje porovnávanie s "podjednotkami" čiže s časťami danej jednotky.
(Pripomeňme, že anglický yard má 3 stopy a každá stopa má 12 palcov). Naša palica má viac ako $1$ yard a $1$ stopu, alebo matematicky vyjadrené má viac ako štyri tretiny yardu. Pri presnejšom meraní (v stopách) má asi $4$ stopy a $5$ palcov, alebo vyjadrené rečou čísel má asi $4$ celé a $5$ dvanástin stopy.

Vo všeobecnosti, ak základná jednotka má $n$ jednotiek nižšieho rádu a meraná veličina je rovná $m$ takýmto nižším jednotkám hovoríme, že jej miera je $\boldsymbol{\frac{m}{n}}$. Tento symbol voláme zlomok, alebo pomer (vtedy ho označujeme $\boldsymbol{m : n}$).
Potreba ďalej narábať s výsledkami meraní postupne (v priebehu dlhých storočí) viedla k abstrahovaniu od procesu merania a výrazy typu $\boldsymbol{\frac{m}{n}}$ sa začali považovať za plnoprávych členov rodiny čísel - za racionálne čísla.
Zamyslime sa podrobnejšie nad najčastejšie používaným vzťahom medzi nejakou veličinou a jej číselnou mierou -
vzťahom medzi úsečkami a ich dĺžkami. Tento vzťah je dvojstranný:
Meranie dĺžok: Úsečke priradíme číslo
Zostrojenie úsečky danej dĺžky: Číslu priradíme úsečku
Na hornom obrázku sme merali dĺžku, teraz naopak zostrojme úsečku, ktorej dĺžka je napríklad $4.4$ jednotiek dĺžky:

Keďže $\boldsymbol{4.4 = 4 \frac{2}{5}}$, jednotkovú úsečku $\boldsymbol{OJ}$ sme naniesli štyrikrát celú a z piatej sme pomocou podobnosti trojuholníkov zostrojili dve pätiny.
"Počítanie" s úsečkami, t.j. zostrojovanie úsečiek, ktorých dĺžka je rovná súčtu, súčinu, podielu, resp. inému zložitejšiemu výrazu z dĺžok daných úsečiek, bolo súčasťou už antickej (gréckej) matematiky.
Na nasledujúcom obrázku sme zostrojili súčet úsečiek $\boldsymbol{Oa + Ob = Oa+b}$, (čiže v našom podaní súčet čísel $\boldsymbol{a + b}$) takým spôsobom, že sme zostrojili stred $\boldsymbol{s}$ úsečky $\boldsymbol{ab}$ a našli sme bod $\boldsymbol{a + b}$ ako súmerný k $\boldsymbol{O}$ podľa stredu $\boldsymbol{s}$. Táto súmernosť zaručuje, že úsečka s koncami $\boldsymbol{b, a + b}$ je rovnako dlhá ako úsečka $\boldsymbol{Oa}$.
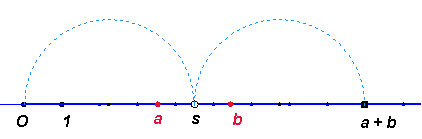
Tu si môžete vyskúšať sčitovanie úsečiek.
Na ďalšom obrázku sme zostrojili úsečku $\boldsymbol{Oab}$, ktorá je súčinom úsečiek $\boldsymbol{Oa, Ob}$. Podobnosť trojuholníkov $\boldsymbol{[O;a;1]}$ a $\boldsymbol{[O;a \cdot b; b']}$ zaručuje, že úsečka $\boldsymbol{Oa \cdot b}$ má dĺžku rovnú súčinu dĺžok úsečiek $\boldsymbol{Oa}$ a $\boldsymbol{Ob}$.
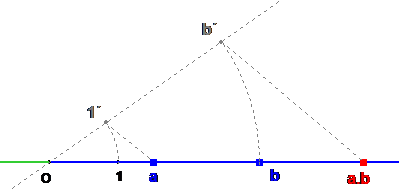
Tu si môžete vyskúšať násobenie úsečiek.