3.1 Riešenie rovníc
Príklad 2.
Vyriešte rovnicu: $\bf{\bbox[yellow]{x + sinx = 2} \qquad (1)}$
Dobrým pomocníkom pri riešení rovníc je tabuľkový kalkulátor EXCEL. Jednoduchou metódou, ktorú sme použili už pri výpočte odmocnín je: $$\bf{Riešenie \; rovnice \; f(x) = 0 \; metódou \; polenia \; intervalu \\ f(x) = x + \sin x - 2 \\ \begin{array} {|c|c|c|c|c|c|} \hline krok & viac \: ako & menej \: ako & rozdiel & (B + C) / 2 & f[(B + C) / 2]\\ \hline 0 & \bbox[aqua, 5px] 1 & \bbox[aqua, 5px] 2 & 1 & 1.5 & 0.497495 \\ \hline 1 & 1 & 1.5 & 0.5 & 1.25 & 0.198985 \\ \hline 2 & 1 & 1.25 & 0.25 & 1.125 & 0.027268 \\ \hline 3 & 1 & 1.125 & 0.125 & 1.0625 & -0.063925 \\ \hline 4 & 1.0625 & 1.125 & 0.0625 & 1.0938 & -0.017895 \\ \hline 5 & 1.09375 & 1.125 & 0.0313 & 1.1094 & 0.004796 \\ \hline \end{array}}$$
Počiatočný odhad je podfarbený modro. Ak je funkčná hodnota v strede intervalu kladná, posunieme do stredu
pravú hranicu intervalu, ak je záporná, posunieme ľavú hranicu do stredu intervalu. Vďaka tomu sa dĺžka
intervalu (ktorý obsahuje riešenie) v každom kroku zmenší na polovicu. Je to primitívna metóda.
pozrite si polenie
Jednoduchší (ale rovnako náročný na čas) je tento spôsob: \begin{array} {|c|c|} \hline x & x + \sin x \\ \hline 1.100 & \bbox[aqua, 5px] {1.99120736} \\ \hline 1.101 & \bbox[aqua, 5px] {1.992660511} \\ \hline 1.102 & \bbox[aqua, 5px] {1.994112769} \\ \hline 1.103 & \bbox[aqua, 5px] {1.995564136} \\ \hline 1.104 & \bbox[aqua, 5px] {1.99701461} \\ \hline 1.105 & \bbox[aqua, 5px] {1.998464191} \\ \hline 1.106 & \bbox[aqua, 5px] {1.999912879} \\ \hline 1.107 & 2.001360672 \\ \hline 1.108 & 2.002807572 \\ \hline 1.109 & 2.004253576 \\ \hline 1.110 & 2.005698686 \\ \hline \end{array}
V hárku odhad zošitu EXCEL sme vypočítali hodnoty výrazu $\bf{x + \sin x}$. Začali sme s prvým odhadom -
intervalom $\bf{(1;2)}$ a so stepom $\bf{0.1}$. V každom ďalšom kroku zúžime interval aj step na desatinu
pôvodnej hodnoty. Po dvoch krokoch sme sa dostali k intervalu $\bf{(1.100 ; 1.110)}$ a stepu $\bf{0.001}$.
Vďaka podfarbeniu buniek s hodnotou menšou ako $\bf{2}$ bezprostredne vidíme, že riešenie našej rovnice je z
intervalu $\bf{(1.106 ; 1.107)}$. Ak si za novú počiatočnú hodnotu stĺpca $\bf{x}$ zvolíte $\bf{1.106}$ a step
zjemníte na $\bf{0.0001}$ (pracujte paralelne aj v Exceli) dostanete presnejší odhad riešenia a síce interval
$\bf{(1.1060 ; 1.1061)}$. Táto napohľad primitívna metóda umožňuje dosiahnuť presnosť na $\bf{n}$ desatinných
miest po $n$ krokoch.
Odhad
Ďalšou, často používanou metódou je iterácia. Pri iterácii sa k výsledku približujeme opkaujúcimi sa rovnakými krokmi. Na obrázku na ďalšej strane, aj v Cabri výkrese Iterácia určujeme priesečník grafu funkcie $\bf{y = \sin x}$ s priamkou $\bf{y = 2 - x}$.
Začíname s nultým odhadom (nultou iteráciou) s bodom na priamke, potom ideme rovnobežne s osou $\bf{y}$, až narazíme na sínusoidu a potom ideme rovnobežne s osou $\bf{x}$, až opäť narazíme na priamku a dostávame prvú iteráciu. Ak budeme pokračovať, dostaneme akúsi do seba zamotanú pravouhlú špirálu, ktorá sa čím ďalej, tým viac približuje k hľadanému priesečníku.
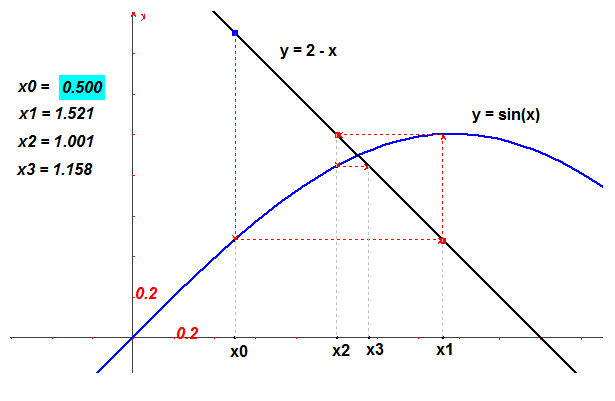
Ak nultá iterácia je $\bf{x_0}$ potom z opísaného postupu aj z obrázku vyplýva, že $\bf{2 - x_1 = \sin x_0, 2 - x_2 = sin x_1, ...}$ resp. všeobecne $\bf{2 - x_{n+1} = \sin x_n}$.
Preto rekurentný vzťah medzi dvoma susednými iteráciami je: $$\bbox[yellow, 5px]{\bf{x_{n+1} = 2 - \sin x_n}}$$
Tento vzťah sme použili v hárku iterácia zošitu EXCEL. I keď je iteračná metóda zdanlivo pomalá,
uvedomte si, že vám stačí pár krokov a miesto pokračovania môžete pružne zmeniť nultý odhad. Pohrajte sa s týmto
hárkom a uvedeným spôsobom vypočítajte riešenie rovnice na 10 desatinných miest.
Iterácia
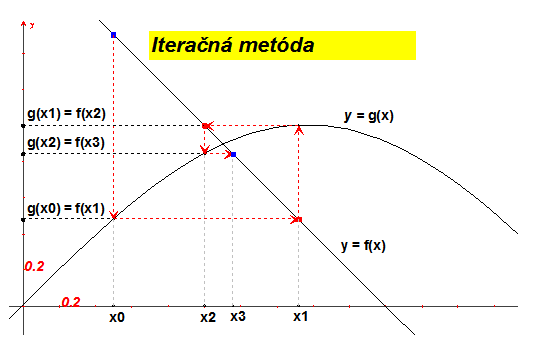
Zovšeobecnime tento postup na hľadanie priesečníka ľubovoľných dvoch funkcií:
Iteračný proces začína voľbou nultej iterácie t.j. bodom na grafe $\bf{f(x)}$, pokračuje bodom na $\bf{g(x)}$ a opäť bodom na $\bf{f(x)}$. Tým jeden iteračný krok končí. Z opísaného postupu aj z obrázk vyplýva, že $\bf{g(x_n) = f(x_{n+1})}$.
Preto rekurentný vzťah medzi dvoma susednými iteráciami je: $$\bf{\bbox[yellow, 5px]{x_{n+1} = f^{-1}(g(x_n))}}$$
Poznámka 3.
Všetky tri uvedené spôsoby (približného) riešenia rovnice $(1)$ vychádzali z dôležitého predpokladu, že v intervale $\bf{(1 ; 2)}$ koreň (a to jediný) existoval. To bolo v našom príklade dôsledkom toho, že graf funkcie $\bbox[yellow, 5px]{\bf{y = x + \sin x - 2}}$ nadobúda v čísle $1$ zápornú a v čísle $2$ kladnú hodnotu a funkcia v tom intervale rastie. Preto na získanie prehľadu a prvej informácie o koreňoch rovnice dobre poslúži pohľad na vhodný graf. Všeobecne, pri riešení rovnice: $$\bf{Ľ(x) = P(x)}$$ si môžeme pomocou vhodného softvéru nakresliť grafy funkcií $\bf{y = Ľ(x), y = P(x)}$ a tak získať informáciu o ich spoločných bodoch, alebo, ak máme jednoduchší softvér, ktorý nevie vypočítať súradnice priesečníka grafov dvoch funkcií, môžeme si nakresliť graf funkcie: $$\bf{y = Ľ(x) - P(x)}$$ a odhadnúť priesečníky (ich počet a polohu) tohto grafu s osou $\bf{x}$.
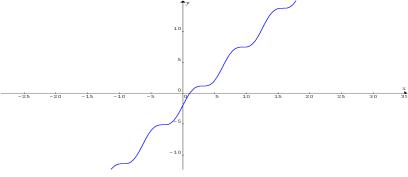
Pohľad na náš obrázok, (t.j. graf funkcie $\bf{y = x + \sin x - 2}$) nás presviedča o tom, že rovnica $(1)$ má
jediné riešenie. Po otvorení projektu G10 (vo free programe DeadLine) kliknutím na voľbu Find roots
dostávame približnú hodnotu koreňa s presnosťou na 8 desatinných miest. Kliknutím na ikonu Graph a
použitím voľby Maximize... dostaneme detailnejší graf, ktorý môžeme podľa potreby upravovať.
G10