MATEMATICKÁ ČÍTANKA

Poznámka 4.

Nájdite reálne číslo, ktorého štvorec zväčšený o trojnásobok tohto čísla je rovný číslu $1$, t. j. vyriešte rovnicu: $x^2 + 3x = 1$. Výsledkom „presného“ riešenia sú čísla $$\bf{x_{1,2} = \frac{-3 \pm \sqrt{13}}{2}} \qquad (^*).$$

Že je to „presné“ riešenie je iba klam. Vzťah $(^*)$ nehovorí nič iné, iba to, že „hľadané číslo vynásobené dvoma a zväčšené o $3$ dá po umocnení na druhú číslo $13$“. My sme iba daný problém previedli na problém „nájsť číslo, ktorého druhá mocnina je $13$“. A ten sa nedá vyriešiť „presne“ žiadnym konečným spôsobom výpočtu. Preto odpor voči približným riešeniam, ktorý majú niektorí matematici – na rozdiel od fyzikov a inžinierov, je zbytočný.

Poznámka 5.

„Není hodno výtečných mužů, aby mařili celé hodiny jako otroci výpočetní dřinou, která by mohla být bezpečně svěřena komukoli jinému, kdyby se používaly stroje.“

Týmito slovami zdôvodňoval Gottfried Wilhelm von Leibniz v roku 1672 svoje pokusy o zostrojenie mechanického kalkulátora. Zoberme si poučenie z jeho slov a ponechajme strojom to, čo patrí strojom a ľuďom to, čo patrí ľuďom. Toho čo môže urobiť (zatiaľ?) len človek je aj tak stále dosť. Preto nepovažujeme za vhodné drezírovať žiakov v riešení najrôznejších druhov rovníc, ale za podstatnú matematickú kompetenciu považujeme schopnosť matematizovať daný problém, schopnosť zostaviť rovnicu, ktorej korene sú riešením problému, resp. nájsť funkciu, ktorej optimálne (pre daný účel) hodnoty sú riešením problému. Toto chceme zdôrazniť aj v nasledovných príkladoch.

Príklad 3.

(pozri Príklad 3. z kapitoly II.1)

Z kruhového výseku kruhu s polomerom $\bf{R}$ zostrojíme plášť kužeľa (pozri obr.). Určte pre akú veľkosť $\bf{\varphi}$ stredového uhla tohto výseku bude objem zostrojeného kužeľa rovný $$\bf{\biggl(\frac{R}{2}\biggr)^3}$$

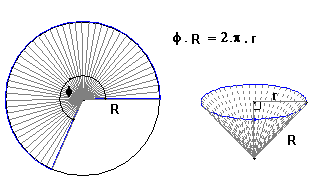
Obvod podstavy hľadaného kužeľa je zrejme $\bf{r = \frac{\varphi R}{2 \pi} }$ a podľa Pytagora pre výšku $\bf{v}$ hľadaného kužeľa platí: $$\bf{v = \sqrt{R^2 - r^2} = \sqrt{R^2 - \biggl(\frac{\varphi R}{2 \pi}\biggr)^2} }$$ Použijúc vzorec pre objem kužeľa dostávame : $$\bf{V(\varphi) = \bbox[yellow, 3px]{\frac{\pi}{3} \cdot \biggl(\frac{\varphi R}{2 \pi}\biggr)^2 \cdot \sqrt{R^2 - \biggl(\frac{\varphi R}{2 \pi}\biggr)^2}}}$$

Keď ako premennú použijeme pomer $\bf{k = \frac{\varphi}{2 \pi} }$, dostaneme: $$\bf{V(k) = \bbox[yellow, 3px]{\frac{\pi}{3} \cdot R^3 k^2 \cdot \sqrt{1 - k^2} } }$$ a máme rovnicu : $$\bf{\bbox[yellow, 3px]{\frac{\pi}{3} \cdot k^2 \cdot \sqrt{1-k^2}} = \bbox[yellow, 3px]{\biggl(\frac{1}{2}\biggr)^3} k \in (0;1) }$$

Lepšie je upraviť pôvodnú rovnicu na tvar $\bf{\bbox[yellow, 3px]{8\pi \cdot k^2 \cdot \sqrt{1-k^2} - 3 = 0 } }$.

Pohľad na graf

nás upozorňuje na dve riešenia, ktoré môžeme získať ako nulový bod grafu funkcie, ktorá je ľavou stranou rovnice. Ak si otvoríte G11, program DeadLine Vám ponúkne riešenie $\bf{k_1 = 0,35751013, k_2 = 0,99263493}$, čo je prevedení na stupne $\bf{\varphi_1 = 128,7^\circ, \varphi_2 = 357,336^\circ}$ .

G11

Druhé riešenie je pomerne nečakané.

Problém.

Máme k dispozícii kartón v tvare kruhu s polomerom $1 \; dm$. Porovnajme dve možnosti:

• kartón rozdelíme na dva polkruhy a z každého urobíme kornútik, t. j. nádobu tvaru kužeľa (pozri predchádzajúci príklad),

• do kruhu vpíšeme pravidelný n–uholník, a z neho urobíme (vystrihnutím deltoidov z jeho rožkov a ohnutím prečnievajúcich častí) škatuľku tvaru pravidelného n–bokého hranola, ako vidíme na obr. dolu. Deltoidy vystrihneme tak, aby podstava vzniknuvšieho hranola bola rozmerovo dve tretiny z pôvodného pravidelného n–uholníka.

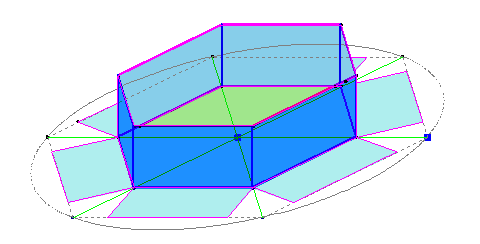
Otázka znie. Môže byť objem takto vzniknuvšieho pravidelného hranola väčší ako súčet objemov kornútikov? Ak áno, tak pre aké $n$?

(Uvedomte si, že jedinou premennou v našom probléme je $\bf{n}$.)

Poznámka 6.

Pri riešení rovníc v predchádzajúcich úlohách použite niektorú z metód použitých pri riešení príkladov 2. a 3.