3.4 Riešenie rovníc s parametrami
Na ukážku vyriešme aj niekoľko „školských“ príkladov typu „debna“.
Príklad 4.
Vyriešte rovnicu s parametrom $\bf{a}$: $$\bf{\sqrt{a - \sqrt{a^2-x^2}} = x}$$
Riešenie:
Skúsme v GeoGebre nakresliť graf $\bf{y = \sqrt{a-\sqrt{a^2-x^2}-x}}$ (závislý na
parametri $\bf{a}$), meniť hodnoty parametra $\bf{a}$ a pozorovať priesečníky grafu
s osou $\bf{x}$.
GeoGebra
Tento spôsob nám umožní pre každú konkrétnu hodnotu parametra nájsť riešenia rovnice (s vyhovujúcou presnosťou), umožní aj realizovať „kvalitatívnu“ diskusiu riešiteľnosti (t. j. zistiť pre aké hodnoty parametra existujú, resp. neexistujú riešenia, aj zistiť ich počet), ale nám neumožňuje určiť akou funkciou parametra sú príslušné riešenia. Pre väčšinu reálnych problémov takéto riešenie vyhovuje.
Príklad 5.
Vyriešte rovnicu s parametrom $\bf{k \in R: \bigg|\sqrt{x^2+x+3}-3\bigg| + |x-2| = k \cdot x + 3 }$.
Riešenie:
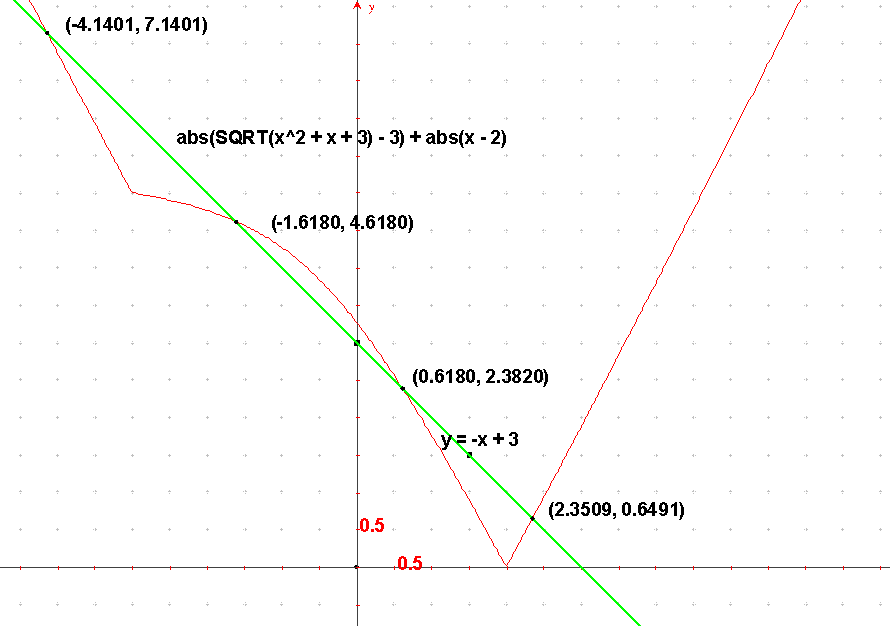
GeoGebra
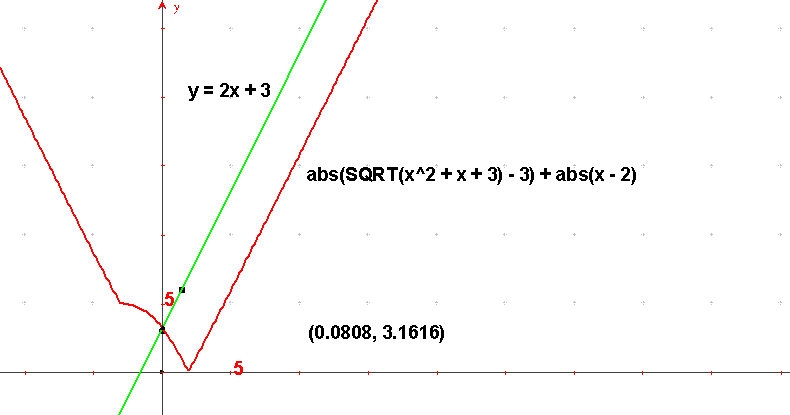
Skúsime ešte EXCEL.
Omylu sa možno vyhneme použitím lepšieho softvéru, ktorý umožňuje väčší „odstup“,
čiže globálnejší pohľad na graf (pozri G12). Ak si súbor otvoríte, môžete si voliť
hodnotu parametra $\bf{k}$ a softvér vám ponúka hľadané korene. Môžete si tiež meniť
tvar grafu podľa Vašich požiadaviek. Pre kritické hodnoty $\bf{k = \pm 2}$ softvér
udáva jediný koreň.
G12
Zdá sa, že bude rozumné vyriešiť konkrétne rovnice pre hodnoty parametru $\bf{k = \pm 2}$.
Pre $\bf{k = 2}$ dostávame $\bf{\bigg\{\sqrt{x^2+x+3}-1\bigg\}+|x-2|=2\cdot x + 3 }$. Pretože hľadáme koreň v intervale $\bf{( 2 ; \infty )}$, kde sú výrazy v oboch absolútnych hodnotách kladné, rovnica má tvar: $\bf{\sqrt{x^2+x+3} = x + 8 }$ čo po ekvivalentnej úprave umocnením dáva $\bf{x+3 = 16x+64}$.
Posledná rovnica očividne v intervale $\bf{( 2 ; \infty )}$ nemá riešenie. (Podobne si doriešte rovnicu pre $k = - 2$ )
Poznámka:
Používanie prostriedkov výpočtovej techniky treba vždy kombinovať so zdravým rozumom. Bez schopnosti vhodne používať ekvivalentné úpravy rovníc a bez primeranej zručnosti s úpravou výrazov nám bude výpočtová technika málo platná.
Úlohy
Vyriešte nasledovné rovnice s parametrami:
-
$bf{\frac{\sqrt{x} - 1 }{\sqrt{x} + 1 } = \frac{a-1}{a+1}}$
-
$\bf{x + \sqrt{x^2+2p^2} = 2p}$
-
$\bf{x + \sqrt{x^2-p^2} = 2p}$
-
$\bf{\sqrt{a- \sqrt{x^2+a^2}} = x}$