3.5 Nerovnosti a nerovnice
Poznámka 1.
Uvedené nerovnosti medzi harmonickým, geometrickým a aritmetickým priemerom ľubovoľných $\bf{n}$ kladných reálnych čísel majú v matematike veľký význam. Pomocou nich, ako aj ďalších: \begin{array}{ll} \bf{\forall a,b \in R: |a+b| \leq |a| + |b|} & \text{(Trojuholníková nerovnosť)}\\ \bf{\forall x \in R, x \gt -1 \land x \neq 0 \forall n \in N, n \geq 2: (1+x)^n \gt 1 +n\cdot x} & \text{(Bernoulliho nerovnosť)}\\ \bf{\forall n \in N \forall a_i, b_i \in R: \bigg(\sum^n_{i=1}a_ib_i\bigg)^2 \leq \bigg(\sum^n_{i=1}a^2_i \bigg) \cdot \bigg(\sum^n_{i=1}b^2_i\bigg) } & \text{(Cauchy – Schwarzova ner.)} \end{array} matematici potvrdili platnosť mnohých tvrdení o funkciách, o rôznych geometrických útvarov a pod. Bez dôkazov tvrdení, na ktoré matematici došli „konštruktívnou intuíciou“, by matematika nebola exaktnou, ale len experimentálnou vedou.
Úlohy
-
Ak $\bf{u = f(a), v = f(b)}$, kde $\bf{y = f(x)}$ je funkcia, ktorá v skúmanej oblasti má kladné hodnoty, tak $\bf{f}$ priemerom čísel $\bf{u, v}$ budeme ho označovať číslo $\bf{f[u; \;v] = f (\frac{a+b}{2})}$.
Vypočítajte $\bf{f[u; \; v]}$ pre funkcie: $\bf{y = x, \; y = 2^2, \; y = \frac{1}{x}}$ a $\bf{y = x^2}$.
Pozrite si Cabri výkres Priemery.
-
Dokážte nerovnosti $(^*)$ pre $\bf{n = 2}$.
-
Dokážte, že pre všetky kladné reálne čísla $\bf{a, b, c}$ platí: $$\text{Ak}\;\bf{a + b + c = 1}\text{,\;tak}\; \bf{ab+bc+ca \leq 1/3}$$
-
Dokážte, že pre všetky reálne čísla $\bf{a_1, a_2, b_1, b_2}$ platí: $$\bf{(a_1b_1+a_2b_2)^2 \leq (a_1^2+a_2^2)\cdot (b_1^2+b_2^2)}$$
Vyriešiť (jednu) nerovnicu s (jednou) premennou $\bf{x}$ (ktorá nadobúda hodnoty z nejakej množiny $\bf{D}$, tzv. „oboru premennej“), znamená nájsť všetky také hodnoty premennej (takzvané riešenie nerovnice), pre ktoré platí: $\bf{Ľ(x) \sim P(x) \land x \in D }$, kde $\bf{Ľ(x)}$ aj $\bf{P(x)}$ sú výrazy premennej $\bf{x}$ a „$\bf{\sim}$“ je jedným zo symbolov $\bf{\leq, \lt, \gt, \geq}$.
Príklad 3.
Vyriešme nerovnicu $\bf{\sqrt{x-3} \geq x - 5}$
-
Klasické riešenie :
Definičným oborom nerovnice je zrejme interval $\bf{\langle 3 ; \; \infty)}$.
Potrebujeme obe strany nerovnice umocniť na druhú. Táto úprava je ekvivalentná len ak sú obe strany nerovnice pre všetky hodnoty premennej nezáporné. To je pravda len v intervale $\bf{\langle 5; \; \infty)}$. Preto definičný obor rozložíme na dve časti:
-
V intervale $\bf{\langle 3; \; 5)}$ nadobúda ľavá strana zrejme nezáporné hodnoty a pravá strana záporné hodnoty, preto tam nerovnosť platí. Máme prvú časť riešenia: $\bf{P_1 = \langle 3; \; 5) }$.
-
V intervale $\bf{\langle 5; \; \infty)}$ b.sú obe strany nezáporné. Po ekvivalentnej úprave (umocnení) dostávane: $\bf{x-3 \geq x^2 - 10x + 25}$ a z toho po ekvivalentnej úprave $\bf{x^2-11x+28 \leq 0}$, resp. $\bf{(x-4)\cdot(x-7)\leq 0 \qquad (^{**})}$
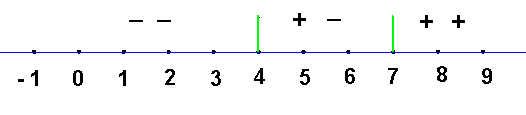
Nahliadnutím do obrázku vidíme, že riešením nerovnice $(^{**})$ je interval $\bf{\langle 4; \; 7 \rangle}$, ale keďže sme v $\bf{\langle 5; \; \infty)}$, je druhou časťou riešenia interval $\bf{P_2 = \langle 5; \; 7 \rangle}$.
Úhrnom, riešením nerovnice je interval $\bf{P = \langle 3; \; 7 \rangle}$.
-
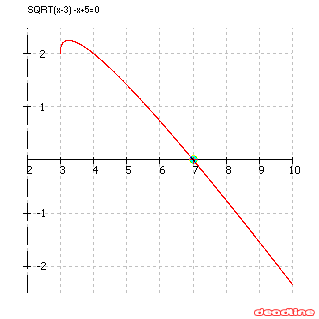
Pravdepodobne jednoduchšie bude upraviť nerovnosť do tvaru $\bf{\sqrt{x-3}-x+5\geq 0 }$ a nakresliť
graf funkcie na ľavej strane (pozri obr.). Riešením je interval $\bf{P = \langle 3; \; 7 \rangle}$,
kde $\bf{7}$ je nulovým bodom funkcie na ľavej strane nerovnice.
Pozrite si tiež G13.