3.5 Nerovnosti a nerovnice
Poznámka 2.
Väčšina reálnych problémov vedie na riešenie nerovníc, ktoré sa ani po vhodných ekvivalentných úpravách nedajú previesť na nerovnicu, ktorú vieme „presne“ vyriešiť pomocou známeho konečného algoritmu. Preto, podobne ako pri riešení rovníc budeme dávať prednosť vhodným približným metódam, používaniu grafov a pod.
Príklad 4.
Vyriešme nerovnicu $\bf{2\sqrt[4]{x-2} - x + 1 \leq 0}$
Najprv sa zorientujeme pohľadom na graf funkcie $\bf{y = 2 \sqrt[4]{x-2}-x+1}$
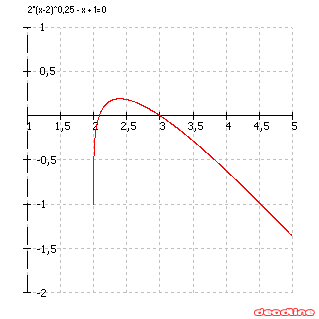
Z grafu vidíme, že riešením bude zjednotenie intervalov: $\bf{\langle 2; \; a \rangle \cup \langle b; \; \infty )}$, kde $\bf{a,b}$ sú riešeniami rovnice $\bf{y = 2 \sqrt[4]{x-2}-x+1 = 0}$.
Pohľad na graf G14 a použitie voľby Find roots dáva dva nulové body:
$$\bf{a = 2.08737083,\; b = 3}$$
G14.
Používanie výpočtovej techniky nám umožňuje riešiť aj nerovnice s parametrom.
Príklad 5.
Vyriešme nerovnicu $\bf{2\sqrt[4]{x-2}-x-q \geq 0 }$ s reálnym parametrom $\bf{q}$.
Riešenie:
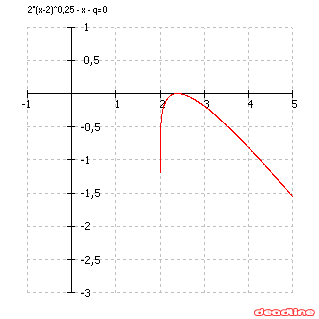
Využili sme možnosti softvéru GeoGebra (otvorte si G15) a nakreslili graf funkcie
$\bf{2\sqrt[4]{x-2}-x-q}$. Softvér umožňuje (digitálne) meniť hodnotu parametra. Na obrázku
vidíte situáciu pre $\bf{q = -0.8095}$ Vtedy softvér dáva dva nulové body funkcie
$\bf{x_1 = 2.38955841 a x_2 = 2.40422112}$
G15.
Aby sme mohli plynulo meniť hodnotu parametra, použijeme Cabri výkres Nerovnice 2.
Nerovnice 2
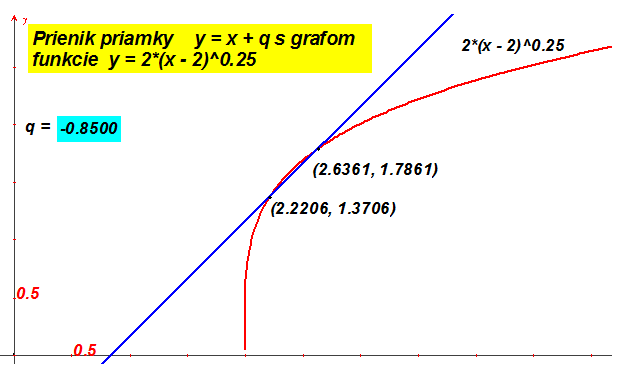
Ak budete manipulovať s hodnotou $q$, zistíte že hraničná hodnota pre parameter $\bf{q}$ je približne $\bf{- 0.8095}$. Pre menšie $\bf{q}$ riešenie nebude existovať, pre $\bf{q}$ niekde v blízkosti tejto hodnoty bude existovať jediné riešenie a potom pre klesajúce $\bf{q}$ bude riešením interval $\bf{\langle a; \; b \rangle}$, resp. pre $\bf{q \leq - 2}$ interval $\bf{\langle 2; \; b \rangle}$, kde $\bf{a, b}$ sú priesečníky priamky $\bf{y = x + q}$ s grafom funkcie $\bf{2\sqrt[4]{x-2}}$
-
Vyriešte nerovnicu s parametrom: $\bf{x + \sqrt{x^2 - p} \geq p}$
-
Vyriešte nerovnicu s parametrom: $\bf{p \cdot x + (p+1) \cdot x \ geq 0 }$
(Pozrite si Nerovnice 2a)