MATEMATICKÁ ČÍTANKA

Obsah

2. Riešenia úloh

  1. Riešenie prémiovej úlohy zasielajte autorovi na adresu +421905332034@orangemail.sk

  2. Kľúčom k riešeniu úlohy je výpočet obsahu trojuholníka $\bf{BYX}$. Pretože priamka $\bf{KL}$ je výsledkom otočenia $\bf{AB}$ o uhol $\bf{\alpha}$, uhol $\bf{BXY}$ má veľkosť $\bf{\alpha}$ a uhol $\bf{KYC}$ a teda aj $\bf{BYL}$ majú veľkosť $\bf{k = \alpha + 60°}$. Z trojuholníka $\bf{BLS}$ sme dostali $\bf{\frac{|BL|}{2} = r \cdot \sin \biggl ( \frac{a}{2} \biggr )}$.

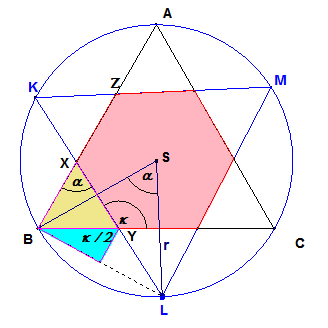
    obrazky

    Z rovnoramenného trojuholníka $\bf{BLY}$ sme vypočítali: $\bf{|BY| = \frac{r \cdot \sin \biggl( \frac{\alpha}{2} \biggr )}{\sin \biggl ( \frac{a}{2} + 30° \biggr )}}$. Zo sínusovej vety pre trojuholník $\bf{BYX}$ sme určili $$\bf{|XY| = |BY|\frac{\sin 60°}{\sin\alpha} = \frac{r \cdot \sin \biggl ( \frac{a}{2} \biggr ) \frac{\sqrt{3}}{2}}{sin \biggl ( \frac{\alpha}{2} + 30° \biggr ) \sin\alpha}}$$

    Potom sme vyjadrili obsah $\bf{T(\alpha)}$ trojuholníka $\bf{BYX}$. $$\bf{T(\alpha) = \frac{|BY||XY|\sin(120° - \alpha)}{2} = \frac{\sqrt 3 r^2}{4} \frac{\Biggl [ \sin \biggl ( \frac{\alpha}{2} \biggr ) \Biggr ]^2 \sin(120° - \alpha)}{\Biggl [ \sin \biggl ( \frac{\alpha}{2} + 30° \biggr ) \Biggr ]^2 \sin \alpha}}$$ Prienik trojuholníkov $\bf{P(\alpha)}$ má obsah $\bf{P_{ABC} - 3 \cdot T(\alpha), P_{ABC} = \frac{3 \sqrt3 r^2}{4}}$. Preto pre hľadaný pomer obsahov $\bf{Q(\alpha)}$ platí: $$\bf{Q(\alpha) = \bbox[yellow, 5px]{1 - \frac{\Biggl [ \sin \biggl ( \frac{\alpha}{2} \biggr ) \Biggr ]^2 sin(120° - \alpha)}{\Biggl [ \sin \biggl (\frac{\alpha}{2} + 30° \biggr ) \Biggr ]^2 \sin\alpha}}, \alpha \in (0°; 120°)}$$ Pozrite si G09 [1] .

    G09

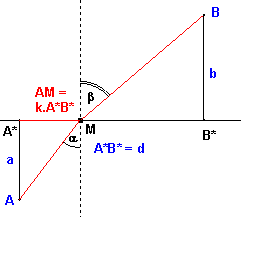
  3. Vyjadrenie pomocou premnnej $\bf{k \in (0; 1)}$ a parametrov $\bf{a, b, d, v_a, v_b:}$ $$\bf{ s(k) = |AM| + |MB| = \sqrt{k^2 d^2 + a^2} + \sqrt{(1 - k)^2 d^2 + b^2}}$$ $$\bf{t(k) = \frac{\sqrt{k^2d^2 + a^2}}{v_a} + \frac{\sqrt{(1 - k)^2 d^2 + b^2}}{v_b}}$$ $$\bf{\frac{\sin\alpha}{\sin\beta} = \frac{k \cdot \sqrt{(1 - k)^2d^2 + b^2}}{(1 - k) \cdot \ sqrt{k^2d^2 + a^2}} }$$

    obrazky

  4. Hľadaná rovnica má tvar: $\bf{\frac{13 880}{x - 1.5} + \frac{15 143}{x} + \frac{16 710}{x + 0.5} = 5000}$, kde $\bf{x}$ je cena plynu v roku $\bf{2003}$.