MATEMATICKÁ ČÍTANKA

Obsah

3.2 Sústavy lineárnych rovníc

Príčina neexistencie jediného riešenia však nemusí spočívať v nedokonalosti nášho algoritmu, ale v samotnej sústave rovníc.

Napr. sústava: \begin{array} {:c:c:} \hdashline 1 & 2 & 3 & 14 \\ \hdashline -2 & -1 & 0 & -4 \\ \hdashline 8 & 7 & 6 & 9 \\ \hdashline \end{array} po pár krokoch dostávame: \begin{array} {:c:c:} \hdashline 1 & 0 & -1 & -2 \\ \hdashline 0 & 1 & 2 & 8 \\ \hdashline 0 & 0 & 0 & -31 \\ \hdashline \end{array} čiže sústavu rovníc, ktorá obsahuje rovnicu $$\bbox[lime, 3px]{\bf{0 \cdot x + 0 \cdot y + 0 \cdot z = -31}} \; \text{,}$$ ktorá evidentne nemá riešenie a preto celá sústava nemá riešenie. Opačným prípadom je sústava: \begin{array} {:c:c:} \hdashline 1 & 2 & 3 & 14 \\ \hdashline -2 & -1 & 0 & -4 \\ \hdashline 8 & 7 & 6 & 40 \\ \hdashline \end{array} Po niekoľkých krokoch dostávame sústavu: \begin{array} {:c:c:} \hdashline 1 & 0 & -1 & -2 \\ \hdashline 0 & 1 & 2 & 8 \\ \hdashline 0 & 0 & 0 & 0 \\ \hdashline \end{array} ktorá obsahuje len dve rovnice. Túto sústavu môžeme upraviť na tvar: \begin{array} {cc} \cellcolor{yellow} x & \cellcolor{yellow} & \cellcolor{yellow} = & \cellcolor{yellow} z & \cellcolor{yellow} - & \cellcolor{yellow} 2 \\ \cellcolor{yellow} & \cellcolor{yellow} y & \cellcolor{yellow} = & \cellcolor{yellow} 2z & \cellcolor{yellow} + & \cellcolor{yellow} 8 \\ \end{array} Vidíme, že sústava má nekonečne veľa riešení, lebo za $\bf{z}$ môžeme zvoliť ľubovoľné reálne číslo.

3. poznámka (pre učiteľov):

Dôkaz toho, že nami sformulované a v predchádzajúcich príkladoch použité úpravy vždy postačia na vyriešenie sústavy lineárnych rovníc, je nad rámec našich doterajších vedomostí. Viac sa o tom dozvieme, keď v knihe „Geometria“ budeme hovoriť o vektoroch.

Pre úspešnosť zvládnutia algoritmu riešenia sústav lineárnych rovníc je dôležitý výber príkladov a úloh. Sprvoti treba zadávať „pekné“ úlohy, t. j. príklady, kde riešiteľ nie je rozptyľovaný vedľajšími problémami (napr. manipuláciou so zlomkami alebo iracionálnymi číslami), sústavy ktoré majú jediné riešenie, proste úlohy, v ktorých sa môže žiak plne sústrediť na sledovanie algoritmu (v našom prípade Jordanovej eliminačnej metódy). Pri výbere a zostavovaní vhodných úloh Vám môže pomôcť jednoduchý generátor úloh, ktorý nájdete v zošite Generovanie1. Generátor pracuje automaticky, pri každej zmene funkcia „RAND“ zmení zadania tam uvedených sústav lineárnych rovníc. Pokúste sa zistiť ako to robí.

Generovanie1

Príklad 3.

Nájdite funkciu, ktorej graf je na obrázku:

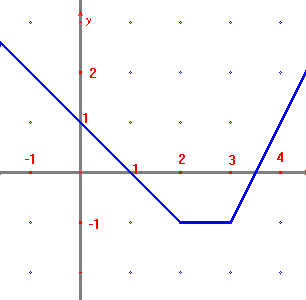
obrazky

Riešenie:

Dá sa predpokladať, že hľadaná funkcia má tvar: $$\bf{y = a |x-2| + b|x-3| \qquad (^*)}$$

Na druhej strane, lomená čiara, ktorá je grafom hľadanej funkcie je jednoznačne určená štyrmi bodmi – prostredná úsečka bodmi $\bf{[2;-1]\text{,} \; [3;-1]}$, a obe krajné polpriamky každá jedným ďalším bodom $\bf{[1;0]\text{,} \; [4;1]}$. Z podmienky, že súradnice týchto bodov majú vyhovovať rovnici $\bf{(^*)}$ by sme dostali štyri rovnice s len dvoma neznámymi. Preto bude rozumné predpokladať, že hľadaná funkcia má tvar: $$\bf{y = a|x - 2| + b|x - 3| + cx + d}$$ z čoho dostávame (po zohľadnení toho, že graf ide cez uvedené body) sústavu rovníc, ktorej matica má tvar: \begin{pmatrix} 1 & 2 & 1 & 1 & 0 \\ 0 & 1 & 2 & 1 & -1 \\ 1 & 0 & 3 & 1 & -1 \\ 2 & 1 & 4 & 1 & 1 \end{pmatrix}

Túto sme vyriešili v zošite MATICE 02.