3.2 Sústavy lineárnych rovníc
Príklad 4.
Vyriešme nasledovné dve sústavy rovníc: $$\begin{array}{:c:c:} \hdashline 2 \cdot x & + & \sqrt{2} \cdot y & & & = & 2 & & & & 2 \cdot x & + & \sqrt{2} \cdot y & & & = & 2\\ \hdashline \sqrt{2} \cdot x & + & 2 \cdot y & + & \sqrt{2} \cdot z & = & 1 + \sqrt{2} & & (Ľ) & & \sqrt{2} \cdot x & + & 2 \cdot y & + & \sqrt{2} \cdot z & = & 2 \cdot \sqrt{2} & & (P)\\ \hdashline & & \sqrt{2} \cdot y & + & 2 \cdot z & = & 2 &&&&&& \sqrt{2} \cdot y & + & 2 \cdot z & = & 2\\ \hdashline \end{array}$$
Keďže ľavé strany sústav sú rovnaké, môžeme ich upravovať naraz. Vynásobme najprv 2. rovnicu (v oboch sústavách) číslom $\bf{\sqrt{2}}$. Dostaneme: $$\begin{array}{:c:c:} \hdashline 2 \cdot x & + & \sqrt{2} \cdot y & & & = & 2 & & & & 2 \cdot x & + & \sqrt{2} \cdot y & & & = & 2\\ \hdashline 2 \cdot x & + & 2 \cdot \sqrt{2} y & + & 2 \cdot z & = & \sqrt{2} + 2 & & (Ľ) & & 2 \cdot x & + & 2 \cdot \sqrt{2} y & + & 2 \cdot z & = & 4 & & (P)\\ \hdashline & & \sqrt{2} \cdot y & + & 2 \cdot z & = & 2 &&&&&& \sqrt{2} \cdot y & + & 2 \cdot z & = & 2\\ \hdashline \end{array}$$
Odčítajme teraz od 2. rovnice (v oboch sústavách) 1. aj 3. rovnicu. Dostaneme: $$\begin{array}{:c:c:} \hdashline 2 \cdot x & + & \sqrt{2} \cdot y & & & = & 2 & & & & 2 \cdot x & + & \sqrt{2} \cdot y & & & = & 2\\ \hdashline 0 \cdot x & + & 0 \cdot y & + & 0 \cdot z & = & \sqrt{2} - 2 & & (Ľ) & & 0 \cdot x & + & 0 \cdot y & + & 0 \cdot z & = & 0 & & (P)\\ \hdashline & & \sqrt{2} \cdot y & + & 2 \cdot z & = & 2 &&&&&& \sqrt{2} \cdot y & + & 2 \cdot z & = & 2\\ \hdashline \end{array}$$
Kým sústava $\bf{(Ľ)}$ očividne nemá riešenie, v riešení sústavy $\bf{(P)}$ môžeme pokračovať. Vypustíme zbytočnú 2. rovnicu a zvyšné dve predelíme číslom 2. Dostaneme: $$\begin{align} \bf{x + \frac{\sqrt{2}}{2}y = 1} & & \bf{\frac{\sqrt{2}}{2}y + z = 1} & & \bf{(P)} \end{align}$$
Zostali nám dve podmienky pre tri neznáme. Zrejme jednu neznámu môžeme ľubovoľne zvoliť a pomocou nej vypočítať zvyšné dve. Ak zvolíme napr. $\bf{y = t}$, dostaneme: $$\begin{align} \bf{x = 1 - \frac{\sqrt{2}}{2}t} & & \bf{y = t} & & \bf{z = 1 - \frac{\sqrt{2}}{2}t} \end{align}$$
Vidíme, že sústava $\bf{(P)}$ má nekonečne mnoho riešení a všetky sa dajú vyjadriť pomocou jedného parametra.
Úlohy
-
Doriešte sústavu rovníc $(S)$ z príkladu 1.
-
Vyriešte tieto dve sústavy $n$ lineárnych rovníc o $n$ neznámych $\bf{(n\in { 3, 4, 5, 6, 7, 8})}$: $$\begin{array}{ll} \text{1. rovnica} & & \bf{x_1 + x_2} & \bf{ = 0}\\ \text{k-ta rovnica} & \bf{k \in {2, 3, ..., n-1}} & \bf{x_{k-1} + x_k + x_{k+1}} & \bf{ = 1 } & \bf{(1)}\\ \text{n-tá rovnica} && \bf{x_{n-1} + x_n} & \bf{ = 0 } \\ \hline \text{1. rovnica} & & \bf{x_1 + x_2} & \bf{ = 2}\\ \text{k-ta rovnica} & \bf{k \in {2, 3, ..., n-1}} & \bf{x_k + x_{k+1}} & \bf{ = 2 } & \bf{(2)}\\ \text{n-tá rovnica} && \bf{x_1 + x_n} & \bf{ = 2 } \\ \end{array}$$
Pozor, počet rovníc je v oboch sústavách dôležitý. (Pozrite si zošit Matice 04, na základe experimentu urobte hypotézu a skúškou dosadením sa presvedčte o jej pravdivosti.)
Matice 04 - 1. list
Matice 04 - 2. list
-
Určte funkciu, ktorej graf je na priloženom obrázku:
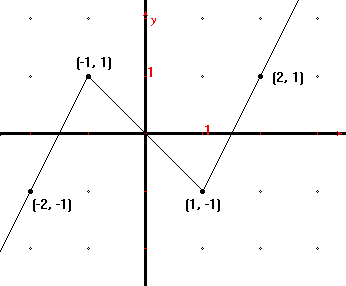
-
Výraz: $\bf{\frac{10x^2 - 16}{x^4 - 5x^2 + 4}}$ rozložte na súčet sčítancov typu $\bf{\frac{A}{x - a}}$
-
Vyjadrite súčet: $\bf{S^3_n = \sum^n_{i = 0}i^3}$ ako polynóm premennej $\bf{n}$.
Záverečná poznámka:
Odkedy existujú také softvéry ako napr. Mathematica, prestáva byť dôležitým mať rutinu s používaním nami uvedenej Jordanovej metódy pri riešení sústav lineárnych rovníc. O to dôležitejšie je rozumieť podstate tejto metódy a naučiť sa používať dostupný softvér. Ak máte v počítači softvér Derive 6, (bol dodaný na všetky stredné školy zapojené do projektu INFOVEK) tak si môžete hravo vyriešiť akúkoľvek sústavu rovníc.