MATEMATICKÁ ČÍTANKA

Príklad 4.

Žiaci dostali za úlohu doniesť príklady rôznych funkčných závislostí z bežného života. Zväčša nosili rôzne cenníky, napr. mobilných operátorov, prehľad z dennej tlače o minimálnych cenách základných potravín v jednotlivých sieťach predajní a pod. Najviac ma zaujal letáčik elektrární, ktorý obsahoval nasledovnú tabuľku: \begin{array}{|c|c|} \hline\text{Sadzba} & \text{Paušál Sk/mes} & \text{24h tarifa Sk/kWh} & \text{Nízka tarifa Sk/kWh}\\ \hline D1 & 8 & 5.4 & - & - \\ \hline D2 & 170 & 3.85 & - & - \\ \hline D12 & 133 & - & 5.4 & 2.05 \\ \hline D22 & 295 & - & 3.85 & 3.05 \\ \hline \end{array}

Tabuľka obsahuje všetku potrebnú informáciu, ale v „skrytej“ podobe. Neumožňuje bezprostredne odpovedať na zásadnú otázku – ktorá sadzba je pre mňa najvýhodnejšia pri danej mesačnej spotrebe.

K tomu bude dobré informáciu zakódovanú v tabuľke odkryť – nejakým prehľadným spôsobom znázorniť závislosť mesačnej platby (pri zvolenej sadzbe) na množstve spotrebovanej energie.

Prvé dve sadzby (závislosť mesačnej platby od mesačnej spotreby) sú lineárne funkcie, ktorých graf sme pomocou Cabri zakreslili na výkrese Funkcie 05.

Paušál platíme aj keď nič nespotrebujeme, preto sme na os y naniesli hodnoty $\bf{8}$ a $\bf{170}$. Tieto body sme posúvali – ak minieme o $\bf{10}\; kWh$ viac (posun doprava o $\bf{10}$), tak sa mi platba zväčší v prípade sadzby $\bf{D1}$ o $54$, v prípade sadzby $\bf{D2}$ o $38,5\; Sk$ (posun hore o $\bf{54}$, resp. o $\bf{38,5}$). Prednosťou Cabri je možnosť voliť vhodnú mierku na jednotlivých súradnicových osiach.

Graf poskytuje dobrý celkový pohľad, ale málo informuje o detailoch. Tie nám lepšie poskytne tabuľka 01 .

Z tabuľky vidieť, že pri spotrebe väčšej ako $104\; kWh$ je sadzba D2 vhodnejšia ako sadzba D1.

Komplikovanejšie je to s ďalšími sadzbami. Tu v závislosti od podielu spotreby vo vyššej tarife z celkovej dennej spotreby (označme ho $p$) priemerná platba za $1\; kWh$ bude: \begin{align} \bf{p \cdot 5.4 + (1-p) \cdot 2.05} \; \text{v sadzbe D12, resp.}\\ \bf{p \cdot 3.85 + (1-p) \cdot 2.05} \; \text{v sadzbe D22.} \end{align}

Grafy závislosti mesačnej platby od množstva spotrebovanej energie vo všetkých sadzbách (pri danom $p$, ktoré môžeme meniť) poskytuje Cabri výkres Funkcie 06.

Funkcie 06

Upozornenie. Vo výkrese sú grafy lineárnych funkcií, ktorých definičným oborom je celá množina reálnych čísel. Ale z kontextu úlohy je zrejmé, že spotreba energie v KWh musí byť nezáporné číslo. Toto (správne určenie oboru premennej) musíme mať na pamäti pri riešení každého problému.

Napriek možnosti interaktívnej voľby parametra $\bf{p}$ a veľkosti jednotky na súradných osiach, je rozlíšenie jednotlivých grafov stále nepohodlné a výhodnejšia je tabuľka 02 . V tabuľkách sme pomocou podmieneného formátovania farebne zvýraznili tú sadzbu, ktorá je pri danej spotrebe najvýhodnejšia.

Príklad 5.

Pán Konček vlastní záhradu. Je pri potoku, má tvar obdĺžnika s rozmermi $30$ krát $35$ metrov a je v nej aj studňa.

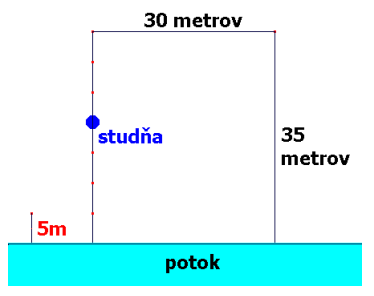
Pán Konček sa rozhodol záhradu rozdeliť medzi svojich dvoch vnukov tak, že časť z ktorej je bližšie k studni bude patriť Andrejkovi a časť z ktorej je bližšie k potoku bude patriť Maťkovi. Sú tu dva problémy:
ako vyzerá deliaca čiara?
kto dostal väčšiu časť záhrady?

Použime program GeoGebra, a nakreslíme si záhradu.

Osádzanie kolov priamo v záhrade pomocou merania vzdialenosti je nepohodlné a namáhavé, skúsme si deliacu čiaru nakresliť najprv na výkrese hranica.

hranica

Krivku, časťou ktorej je deliaca čiara, matematici volajú parabola, alebo presnejšie: Množina bodov v rovine, ktoré majú rovnakú vzdialenosť od daného bodu F a od danej priamky (ktorá neprechádza bodom F) d voláme parabola. Bod F sa volá ohnisko paraboly a priamka d riadiaca priamka paraboly.

Ako vidíme na obrázku, parabola je súmerná podľa priamky idúcej cez ohnisko kolmo na riadiacu priamku. Túto priamku voláme os paraboly. Bod na osi voláme vrchol paraboly.

parabola

Prvý problém s deliacou čiarou je vyriešený. Vieme bod po bode zostrojiť našej potrebe primeraný počet bodov paraboly, tam napr. zatĺcť koly a použitím drôteného pletiva zostrojiť plot.

Na riešenie druhého problému budeme potrebovať matematické vyjadrenie paraboly, t. j. nejaké kritérium, pomocou ktorého zistíme ktorý bod roviny parabole patrí a ktorý nie. K tomu si vhodne zvolíme súradnicovú sústavu.

Pozrime si výkres: rovnica

Experimentovanie v tomto výkrese je poučné:

Ak si nastavíte vzdialenosť ohniska od riadiacej priamky rovnú $\bf{0,5}$ (polparameter $\bf{p}$ bude mať hodnotu $\bf{0,25}$), tak v súradnicovej sústave so začiatkom vo vrchole paraboly a s osou $y$ totožnou s jej osou, je závislosť medzi súradnicami bodov paraboly vyjadrená vzťahom: $\bf{y = x^2}$

Voľte postupne za hodnoty polparametra $p$ čísla $\bf{0,1; 0,25; 0,5; 1; 2}$ a v každej voľbe meňte hodnoty premennej $\bf{x}$ od $\bf{-1}$ do $1$ s krokom po jednej desatine.

Výsledky porovnávajte s tabuľkou.

V nej je prehľadne vyjadrená závislosť medzi súradnicami $x$ a $y$ bodov paraboly v závislosti na hodnote polparametra $p$.

Z uvedenej tabuľky plynie, že je oprávnená hypotéza:

Ak vzdialenosť medzi ohniskom a riadiacou priamkou paraboly je 2p, tak parabola má v súradnicovej sústave so začiatkom vo svojom vrchole a s osou y totožnou so svojou osou rovnicu: $\bf{y=x^2/4p}$