MATEMATICKÁ ČÍTANKA

Obsah

4.1 Polynomické funkcie

Úlohy

  1. Otvorte si pracovné listy PL01 a PL02.

    PL01
    PL02
    Konajte podľa pokynov tam uvedených tak, aby ste mohli správne doplniť nasledovné tvrdenia:

    • Paraboly $\bf{y = a \cdot x^2 + b \cdot x + c}$ a $\bf{y =p\cdot x^2 + q \cdot x + r}$ sú zhodné (majú rovnaký parameter a teda aj tvar) práve vtedy keď .........

    • Paraboly $\bf{y = a \cdot x^2 + b \cdot x + c}$ a $\bf{y =u\cdot (x-v)^2 + w}$ sú totožné (splývajú) práve vtedy keď ........

  2. Pozrite si výkres Odraz a vysvetlite, prečo reflektory (predné svetlá ) automobilov majú v priereze tvar paraboly.

    Odraz

Kreslenie grafov funkcií

Existujú viaceré matematické i didaktické softvéry, ktoré umožňujú presne a rýchlo nakresliť graf žiadanej funkcie. Mnohé ponúkajú možnosti

  • určiť priesečníky viacerých grafov, resp. aspoň priesečníky s osou x,

  • určiť extrémy,

  • v ľubovoľnom bode zostrojiť dotyčnicu,

  • určiť funkciu, ktorá je deriváciou danej funkcie, alebo funkciou k nej primitívnou,

  • vypočítať určitý integrál vo zvolených hraniciach.

Za všetky spomeňme aspoň DERIVE 6, ktorý je dodávaný na školy zapojené do projektu INFOVEK a GeoGebra, ktorú používame v tomto texte.

Cabri nie je vhodný softvér na kreslenie grafov funkcií v situáciách, keď riešime reálny problém. Pomocou Cabri však môžeme pochopiť podstatu pojmu funkcia, kresliť grafy parametrických súborov funkcií, a kresliť aj grafy takých funkcií, ktoré sú definované inak ako vzorcom pre výpočet y pomocou x (ako napr. grafy funkčných závislostí z príkladov 1 a 2).

S pomocou ikon „výraz“ a „použi výraz“ môžeme nakresliť graf ľubovoľnej funkcie, ktorej výroková forma sa dá vytvoriť pomocou základných operácií a zátvoriek z funkcií uvedených v takej podobe, ako sa nachádzajú v Cabri ikone „kalkulačka“.

Pozrite si Graf 1.
Zmenu grafu docielite zmenou samotného výrazu. Hypotézu o tvare grafu a jeho významných bodoch, ktoré získate z nakresleného grafu môžete doplniť úvahou, výpočtom a dokreslením význačných bodov aj s ich súradnicami.

Môžeme nakresliť aj graf funkcie závislej na parametroch. Tieto parametre môžeme určiť ako meniteľné číselné hodnoty ako to je v Cabri výkrese Graf 2. Ak budete v tomto výkrese meniť hodnoty parametrov, graf funkcie sa Vám bude priebežne meniť.

Graf 2.

Parametre je možné zadať aj ako dĺžky úsečiek či ako súradnice bodov, ktoré môžeme meniť (spojite) pohybom myši. Dobre je to vidieť na výkrese Graf 3. Pohrajte sa s ním.

Graf 3.

Poznámka

Funkcia na výkrese Graf 2 sa volá polynomická funkcia, na výkrese Graf 3 lineárne lomená funkcia a takej funkcii aká je na výkrese Graf 1 hovoríme iracionálna funkcia.

Úlohy

  1. Otvorte si výkres Graf 3 a odpovedzte na nasledovné otázky o funkcii $\bf{y = \frac{ax+b}{x+c}}$:

    Graf 3.

    • Pre ktorú hodnotu $\bf{x}$ nie je definovaná?

    • Akú hodnotu $\bf{y}$ nikdy nenadobudne?

    • Pre aké $\bf{k}$ je graf funkcie $\bf{y = \frac{k}{x}}$ zhodný s grafom funkcie $\bf{y = \frac{ax+b}{x+c}}$?


Príklad 7.

Nakreslite graf polynomickej funkcie čo najmenšieho stupňa, ktorej graf prechádza bodmi $$\bf{A[-2;\;4],\;B[-1;\;-1],\;C[1;\;1],\;D[3;\;9] \qquad(\clubsuit)}$$

Riešenie

Najprv uvažujme. Z podmienok, že uvedené body patria danej funkcii dostaneme 4 rovnice pre koeficienty hľadaného polynómu. Preto je rozumné predpokladať, že to bude polynóm 3. stupňa. Skúsme experimentovať. Otvorme si výkres Graf 2, v ktorom je graf funkcie: $$\bf{y = A_3x^3 + A_2x^2 + A_1x + A_0 \qquad(\heartsuit)}$$

Graf 2.
vyznačme v ňom dané body a experimentujme s hodnotami parametrov $\bf{A_i}$. Myslím, že po chvíli trápenia ste pochopili, že toto nie je schodná cesta. Ak do vzťahu $(\heartsuit)$ dosadíme postupne súradnice $(\clubsuit)$ dostaneme sústavu rovníc s maticou: \begin{array}{:c:c|c:}\hdashline \cellcolor{cyan}\bf{-8} & \cellcolor{cyan}\bf{4} & \cellcolor{cyan}\bf{-2} & \cellcolor{cyan}\bf{1} & \cellcolor{cyan}\bf{4} \\ \hdashline \cellcolor{cyan}\bf{-1} & \cellcolor{cyan}\bf{1} & \cellcolor{cyan}\bf{-1} & \cellcolor{cyan}\bf{1} & \cellcolor{cyan}\bf{-1} \\ \hdashline \cellcolor{cyan}\bf{1} & \cellcolor{cyan}\bf{1} & \cellcolor{cyan}\bf{1} & \cellcolor{cyan}\bf{1} & \cellcolor{cyan}\bf{1} \\ \hdashline \cellcolor{cyan}\bf{27} & \cellcolor{cyan}\bf{9} & \cellcolor{cyan}\bf{3} & \cellcolor{cyan}\bf{1} & \cellcolor{cyan}\bf{9} \\ \hdashline \end{array}

Riešenie tejto sústavy si môžete pozrieť v zošite Polynom1.

Polynom1
Ak výsledné hodnoty $$\bf{A_3 = - 0.25, \; A_2 = 1.5, \; A_1 = 1.25, \; A_0 = -1.5}$$ dosadíte do výkresu Graf 2, utvrdíte sa v správnosti nášho riešenia.
Graf 2.


Úlohy.

  1. Nakreslite graf polynomickej funkcie čo najmenšieho stupňa, ktorej graf prechádza bodmi $$\bf{A[-2; \; -33],\; B[-1;\;-3],\;C[1;\;3],\;D[2;\;-9],\;E[3;\;-63]}$$

  2. Nakreslite graf funkcie $\bf{y = \frac{ax+b}{ax+c}}$, ak jej graf prechádza bodmi $\bf{A[1;\;4],\;B[2;\;3],\;C[3;\;2]}$

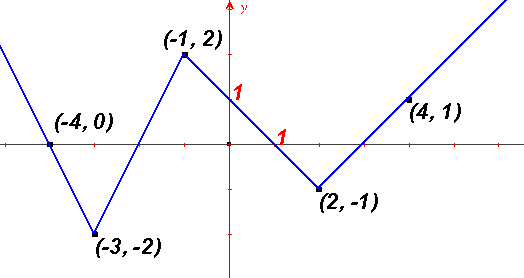
  3. Určte funkčný predpis funkcie, ktorej graf vidíte na obrázku.

    obrazky