4.1 Polynomické funkcie
Poznámka
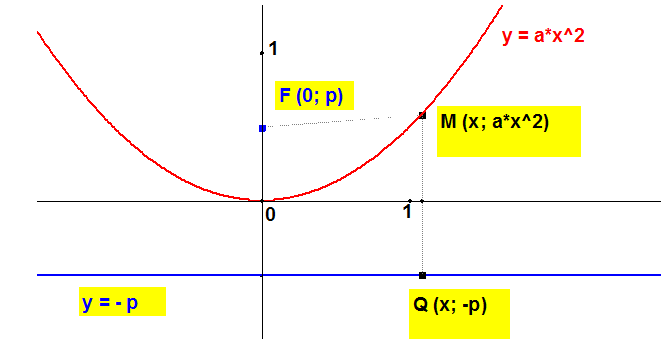
Uvedenú hypotézu ľahko dokážeme ak si pozorne všimneme obrázok:
Otázka znie: Aká musí byť hodnota parametra $a$, aby sa dĺžky úsečiek $FM$ a $QM$ rovnali pre ľubovoľnú hodnotu premennej $x$?
Porovnaním štvorcov týchto dĺžok dostávame:
$\bf{(x-0)^2 + (a\cdot x^2 -p)^2 = (a\cdot x^2 + p)^2}$, po umocnení a malej úprave dostávame $\bf{x^2=4\cdot a \cdot p \cdot x^2}$
Z rovnosti pre ľubovoľné $\bf{x}$ plynie podmienka: $\bf{p = \frac{1}{4a}}$
Čo sme chceli dokázať.
Rovnicu paraboly, ktorá je deliacou čiarou, určíme ak do úvodného obrázku vložíme vhodne súradnicovú sústavu:
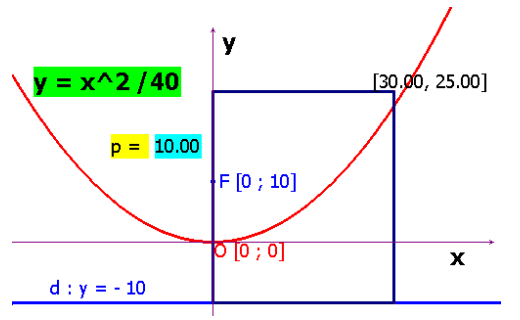
Príklad 6.
Do podkrovného priestoru chceme zabudovať skladový priestor tvaru kvádra čo najväčšieho objemu:
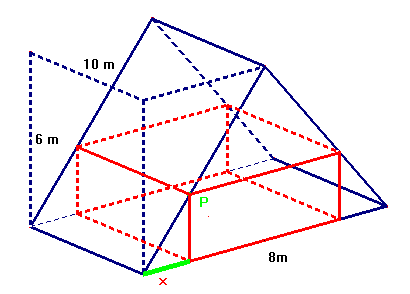
Skôr než sa pokúsime vyjadriť objem skladového priestoru pomocou premennej x, pozrime si výkresy:
Vidíme, že objem bude maximálny, keď bude maximálny obsah obdĺžnika v prednej stene. Preto sa pozrime na obrázok:
Podkrovie2
Podkrovie3
Z obrázku vo výkrese Podkrovie vyplýva, že závislosť obsahu obdĺžnika vpísaného do trojuholníka od polohy bodu $P$, t. j. od dĺžky $x$ je vyjadrená vzťahom: $$\bf{S = (8 - 2 \cdot x) \cdot 1.5x = -3x^2 + 12x}$$
Poznámka:
Takejto závislosti hovoríme že $S$ je kvadratickou funkciou premennej $x$. V príklade 5. sme zistili, že grafom takejto závislosti je parabola.