1.3 Diery v číselnej osi alebo iracionálne čísla
Predchádzajúce príklady nás presviedčajú o tom, že racionálne čísla nepostačujú na meranie dĺžok. Inak povedané, existujú úsečky, ktorých dĺžka nie je racionálne číslo. Otázka je ako má vyzerať tá množina čísel, pomocou ktorej sa dá odmerať ľubovoľná dĺžka. Návod poskytuje grafické sčitovanie a grafické násobenie (pozri Q++ a Qx). Tam je výsledok závislý iba na polohe sčítancov (či súčiniteľov) na číselnej osi a nezávisí na tom, či sú tieto body (t.j. sčítance, resp. súčinitele) obrazmi racionálnych čísel, alebo nie. Preto hľadaná množina čísel by mala byť rovnocenná s množinou všetkých bodov priamky. (T.j. každé číslo by malo práve jeden obraz na priamke a každý bod priamky by bol obrazom práve jedného čísla.)
Q++
Qx
Takéto intuitívne ponímanie nových čísel dlho postačovalo matematikom na to, aby dosahovali významné objavy. Tie čísla, ktoré sa dajú vyjadriť ako zlomok, teda také, ktoré sa dajú vyjadriť ako konečné desatinné číslo, alebo nekonečné ale periodické desatinné číslo sú racionálne čísla a čísla, ktoré sa nedajú vyjadriť ako zlomok, teda také, ktorých desatinný rozvoj nie je konečný a ani nekonečný periodický, dostali názov iracionálne. Nová množina čísel, skladajúca sa z racionálnych aj iracionálnych čísel dostala názov reálne čísla. Pojem reálneho čísla matematici [ 1, 1 ] presne formulovali až v XIX storočí. O tom si povieme niečo viac v kapitole Limitné procesy.
Príklad 4.
Otvorme si zošit Uhlopriečka list 1. a zapisujme postupne čoraz menšie intervaly, ktoré ohraničujú číslo, ktorého druhá mocnina je 5. Postupným zjemňovaním kroku dostávame: $$\bf{(2 \, ; \, 3), \, (2.2 \, ; \, 2.3), \, (2.23 \, ; \,2.24),}$$ $$\bf{(2.236 \, ; \, 2.237), \, (2.2360 \, ; \, 2.2361), \, (2.23606 \, ; \, 2.23607), \, ...}$$
Uhlopriečka list 1
Aby sme teda mohli hovoriť o druhej odmocnine (z ľubovoľného čísla, nielen z piatich), musí platiť: V množine reálnych čísel existuje jediné číslo, ktoré patrí do všetkých takýmto spôsobom získaných intervalov.
Poznámka 1.
Posledná vlastnosť je práve tou vlastnosťou, ktorá odlišuje množinu všetkých reálnych čísel (označujeme ju $\mathbb{R}$) od množiny $\mathbb{Q}$. Táto vlastnosť nám zaručuje napríklad existenciu ľubovoľnej odmocniny z ľubovoľného kladného reálneho čísla: $$\bbox[yellow, 5px] {\bf{\forall \, a, b \in \mathbb{R}^+ \forall \, q \in \mathbb{N} : b = \sqrt[q]{a} \iff b^q = a \qquad{(DO)}}}$$
Príklad 5.
Spôsob, ako postupne spresňovať hodnotu druhej odmocniny z ľubovoľného kladného čísla realizovaný v zošite Uhlopriečka je nešikovný a zdĺhavý. Uvedieme niekoľko ďalších. Vypočítať $\bf{\sqrt{a}}$ znamená vyriešiť rovnicu $\bf{x ^ 2 - a = 0}$ (na obrázku sme zvolili $\bf{a = 5}$)
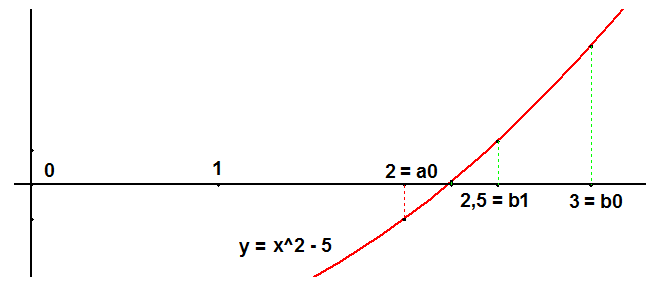
Najprv zvolíme 1. odhad $\bf{(a_0, b_0)}$ intervalu, v ktorom sa nachádza koreň rovnice $\bf{f(x) = 0}$, (t.j. bod, v ktorom graf funkcie $\bf{y = f(x)}$ pretína os $\bf{x}$). Dbáme o to, aby v krajných bodoch nadobúdala funkcia hodnoty opačných znamienok, napr. $\bf{f(a_0) \lt 0}$ a $\bf{f(b_0) > 0}$. Interval rozpolíme, vypočítame hodnotu v jeho strede a z intervalov $\bf{(a_0,(a_0 + b_0) / 2), ((a_0 + b_0) / 2, b_0)}$ vyberieme ten, v ktorého koncových bodoch nadobúda funkcia opačné znamienko. Takto pokračujeme dovtedy, kým nedosiahneme požadovanú presnosť. Prvé kroky tejto metódy vidíme na obrázku, priebeh môžeme sledovať v Exceli v 1. liste zošitu Odmocnina.
Odmocnina list 1