1.3 Diery v číselnej osi alebo iracionálne čísla
Poznámka
Vzťahy $\bf{p = m - n, q = 2n - m}$ sú zaujímavé. Otvorte si zošit SQRT(2), sú v ňom dve postupnosti, $\bf{a(n)}$ a $\bf{b(n)}$ definované takto: $$\bf{a(n + 1) = b(n) - a(n),}$$ $$\bf{b(n + 1) = 2 \cdot a(n) - b(n)}$$
SQRT(2)
Zaujímavé je, že bez ohľadu na to, ako zvolíte prvé členy týchto postupností, číslo $\bf{\biggl | \frac{a(n)}{b(n)} \biggr |}$ sa bude vždy približovať (už pre malé $n$) k druhej odmocnine z dvoch.
Príklad 2.
Ukážeme ešte jeden dôkaz tvrdenia, že neexistuje také racionálne číslo $\bf{u}$, pre ktoré platí $\bf{u^2 = 2}$.
Podobne, ako v predchádzajúcom príklad použijeme tzv. dôkaz sporom:
Predpokladajme, že také racionálne číslo $\bf{u}$ existuje, t.j. existujú také prirodzené čísla $\bf{a, b}$,
pre ktoré platí: $\bf{\biggl (\frac{a}{b} \biggr )^2 = 2}$ a súčasne sú čísla $\bf{a, b}$ nesúdeliteľné.
(Proste zo všetkých zlomkov požadovanej vlastnosti vyberieme ten, ktorý sa už nedá krátiť.) Potom ale
$\bf{a^2 = 2 \cdot b^2}$, čiže číslo $\bf{a^2}$ je párne. Z toho ale vyplýva, že aj $\bf{a}$ musí byť
párne[2], teda $\bf{a = 2 \cdot c}$. Ak to dosadíme
do predchádzajúcej rovnice dostaneme $\bf{4 \cdot c^2 = 2 \cdot b^2}$, alebo po úprave
$\bf{b^2 = 2 \cdot c^2}$ čiže aj číslo $\bf{b}$ je párne. Teda zlomok $\bf{\frac{a}{b}}$ sa dá krátiť, čo
je v spore s predpokladom.
Úlohy
-
Dokážte, že neexistuje také racionálne číslo $\bf{b}$, pre ktoré platí $\bf{b^2 = p}$ (kde $\bf{p}$ je ľubovoľné prvočíslo). (Použite tvrdenie z príkladu 6 z kapitoly 1.1)
Príklad 3.
Jedným z klasických problémov gréckej matematiky bola tzv. duplicita kocky. Možno ho zjednodušene vysloviť takto - zostrojte kocku, ktorej objem je dvojnásobok objemu jednotkovej kocky. Našimi slovami - nájdite také číslo $a$, ktorého tretia mocnina je $2$.
Grécki matematici na to používali nástroj zvaný križiak, ktorého virtuálnu
podobu nájdete tu.
Z podobnosti trojuholníkov vyplýva, že odvesny všetkých trojuholníkov sú v pomere $\bf{1:a}$.
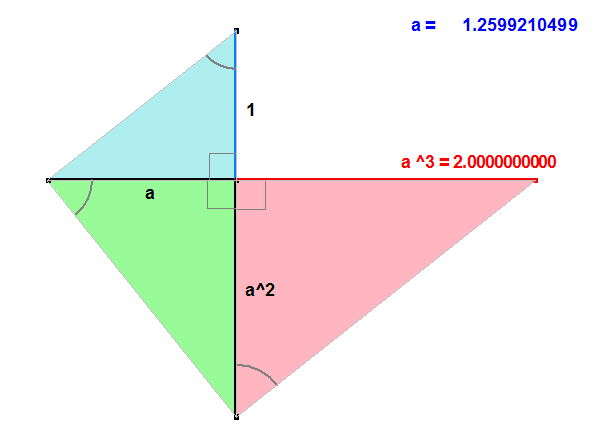
Otvorte si výkres Križiak a pomocou neho vypočítajte $\bf{\sqrt[3]{2}}$ s presnosťou na desať desatinných miest.
križiak
Pri riešení ďalších klasických problémov, ako boli kvadratúra kruhu a rektifikácie kružnice, starí Gréci zistili, že čísla vyjadrujúce pomer obsahu kruhu ku obsahu jednotkového štvorca a tiež pomer obvodu kružnice k jej priemeru nie sú (v našom označovaní) racionálne.
Úlohy
-
Otvorte si zošit Uhlopriečka a upravte podmienené formátovanie buniek $B5$ až $B15$ tak, aby ste pomocou tohto zošitu mohli demonštrovať postupné spresňovanie výpočtu druhej odmocniny z ľubovoľného prirodzeného čísla. (Ak sa Vám to nepodarí, pozrite si List2.)
Uhlopriečka
List2
-
Pomocou zošitu Uhlopriečka vypočítajte druhé odmocniny z prirodzených čísel do $10$ s presnosťou na $10$ desatinných miest.
Uhlopriečka
-
Pomocou Cabri výkresu Križiak vypočítajte s presnosťou na $10$ desatinných miest tretie odmocniny z prirodzených čísel do $10$.
križiak
-
Doplňte výkres Križiak o ďalší podobný trojuholník tak, aby ste pomocou neho mohli počítať štvrté odmocniny.
križiak