MATEMATICKÁ ČÍTANKA

Príklad 3.

Z kruhového výseku kruhu s polomerom $1$ zostrojíme plášť kužeľa (pozri obr.). Vyjadrite objem tohto kužeľa pomocou veľkosti stredového uhla výseku.

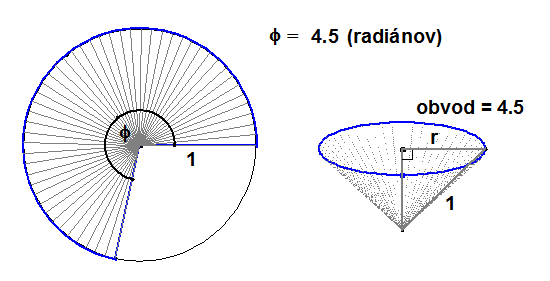
Obvod podstavy hľadaného kužeľa je zrejme $\bf{\varphi = 2 \pi \cdot r \Rightarrow r = \frac{\varphi}{2\pi}}$ a podľa Pytagora pre výšku $\bf{v}$ hľadaného kužeľa platí: $\bf{v = \sqrt{1 - r^2} = \sqrt{1 - \bigg(\frac{\varphi}{2\pi} \biggr )^2}}$. Použijúc vzorec pre objem kužeľa dostávame: $$\bf{V(\varphi) = \bbox[yellow, 5px]{\frac{\pi}{3} \cdot \biggl (\frac{\varphi}{2\pi} \biggr )^2 \cdot \sqrt{1 - \biggl (\frac{\varphi}{2\pi} \biggr )^2}}}$$

Vidíme, že nae vyjadrenie obsahu by bolo výrazne jednoduchšie, keby sme ako premennú neuvažovali veľkosť stredového uhla $\bf{\varphi}$ kruhového výseku, ale pomer $\bf{k = \frac{\varphi}{2\pi}}$. Potom by pre objem platilo: $$\bf{V(k) \bbox[yellow, 5px] {\frac{\pi}{3} \cdot k^2 \cdot \sqrt{1 - k^2}}}$$ (Môžete si pozrieť výkres Objem kužeľa.)

Príklad 4.

Na rovine je položená guľa s jednotkovým polomerom. Treba ju prikryť plášťom kužeľa tak aby guľa bola vpísaná do kužeľa. Vyjadrite povrch plášťa pomocou:

1. polomeru $\bf{r}$ podstavy kužeľa
2. výšky $\bf{v}$ kužeľa
3. veľkosť uhla $\bf{\alpha}$, ktorý zvierajú povrchové priamky kužeľa s jeho osou.

Na obrázku na ďalšej strane máte prierez kužeľa a rozvinutý plášť kužeľa v príslušnej mierke. Obrázok si tiež môžete pozrieť na výkrese Plášť kužeľa. V tomto výkrese môžete meniť myšou polohu vrcholu $\bf{V}$ kužeľa a sledovať ako sa menia ostatné veličiny, vrátane rozvinutého plášťa.

Pre povrch $\bf{P}$ plášťa kužeľa, ktorého podstava má polomer $\bf{r}$ zrejme platí: $$\bf{P = \pi s^2 \cdot \frac{2 \pi r}{2 \pi s} = \pi r s}$$

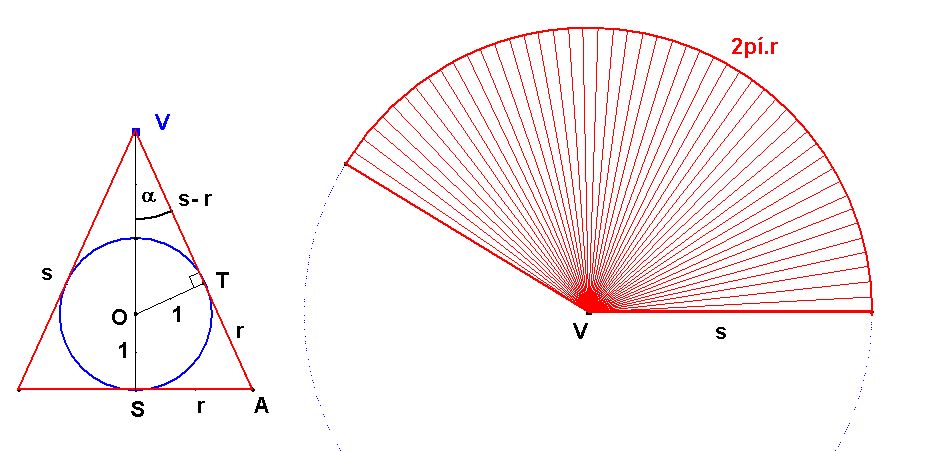
Z podobnosti trojuholníkov $\bf{OTV}$ a $\bf{ASV}$ dostávame vzťahy: $$\bf{\bbox[yellow, 5px]{\frac{1}{r} = \frac{s - r}{|SV|} = \frac{|SV| - 1}{s}} \qquad (1)}$$

Z nich sa pokúsime vyjadriť povrch plášťa kužeľa:

1. pomocou $\bf{r}$

2. pomocou $\bf{v = |SV|}$

3. pomocou $\bf{\alpha}$

1. Z (1) $\Rightarrow \bf{s = r \cdot v - r}$ (2) a tiež $\bf{v = r \cdot s - r^2}$ (3). Ak do (2) dosadíme za $\bf{v}$ z (3), dostávame $\bf{s = r(rs - r^2) - r}$ $\bf{ \Rightarrow s = r^2s - r^3 - r \Rightarrow r^3 + r = (r^2 - 1)s \Rightarrow s = \frac{r^3 + r}{r^2 - 1}}$ Odtiaľ pre povrch plášťa dostávame: $\bf{P(r) = \pi r s = \bbox[yellow, 5px]{\pi r^2 \frac{r^2 + 1}{r^2 - 1}}, r \in (1; \infty) \qquad (4)}$

2. Ak do (3) dosadíme za $\bf{s}$ zo vzťahu (2), dostávame: $\bf{v = r(rv - r) - r^2 \Rightarrow v = r^2 v -2r^2}$.

   Z tohto vzťahu určíme $\bf{r^2 = \frac{v}{v-2}}$ 2.a toto dosadíme do (4). Postupne dostávame: $$\bf{P(v) = \pi \frac{v}{v-2} \frac{\frac{v}{v - 2} + 1 }{\frac{v}{v - 2} -1 } = \pi \frac{v}{v-2} \frac{v + v - 2}{v - v + 2} = \bbox[yellow, 5px]{\pi \frac{v (v-1)}{v-2}} v \in (2; \infty) \qquad (5) }$$

3. Z trojuholníka $\bf{OTV}$ máme $\bf{\sin \alpha = \frac{1}{v - 1} (6) }$ a z trojuholníka $\bf{ASV}$ máme $\bf{\cos \alpha = \frac{v}{s} (7)}$ $$\bf{(6) \Rightarrow v - 1 = \frac{1}{\sin \alpha} \Rightarrow v = \frac{1}{\sin \alpha} + 1 = \frac{\sin \alpha + 1}{\sin \alpha} },$$ $$\bf{(7) \Rightarrow s = \frac{v}{\cos \alpha} = \frac{\sin \alpha + 1}{\sin \alpha \cos \alpha}}.$$ Z posledných dvoch vzťahov dostávame: $$\bf{P(\alpha) = \pi r s = \bbox[yellow, 5px]{\pi \frac{(\sin \alpha + 1)^2}{\sin \alpha \cos^2 \alpha} \; \alpha \in \biggl(0; \frac{\pi}{2}\biggr) } \qquad (8) }$$

Definičné obory premenných sú zrejmé. Získané vyjadrenia sú prekvapujúco málo podobné. Ak si pozriete grafy G05a, G05b, G05c, pomocou ikony „Calculate“ a voľby „Find extrema“ zistíte, čo je od voľby premennej nezávislé.