MATEMATICKÁ ČÍTANKA

Úlohy

1. Vyjadrite povrch plášťa kužeľa z predchádzajúceho príkladu pomocou pomeru $\bf{\frac{r}{s}}$.

   Pokúste sa pomocou GeoGebry nakresliť graf tejto závislosti.

2. Na rovine je položená polguľa s jednotkovým polomerom. Treba ju prikryť plášťom kužeľa tak, aby polguľa bola vpísaná do kužeľa.

   

   Vyjadrite povrch plášťa pomocou:

   • polomeru podstavy $\bf{r}$ kužeľa

   • výšky $\bf{v}$ kužeľa

   • veľkosti uhla $\bf{\varphi}$, ktorý zvierajú povrchové priamky kužeľa s jeho osou.

   Pozri tiež Pokrytie polgule

   
   

   pracuje sa na tom

3. Máme pružnú tyč dĺžky $\bf{d = 10 m}$. Tyč má takú vlastnosť, že nech ju akokoľvek ohneme (priblížime k sebe jej konce), vždy bude tvoriť časť kružnice.

   

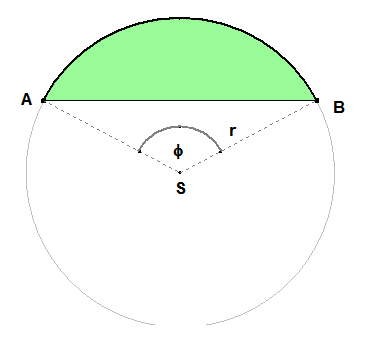
   Vyjadrite obsah odseku nad tetivou $\bf{AB}$ pomocou:

   • Veľkosti stredového uhla $\bf{\varphi}$

   • Polomeru krivosti $\bf{r}$

   Pozri tiež Ohýbanie tyče

   
   

   Prémia: Vyjadrite obsah odseku pomocou dĺžky tetivy $\bf{AB}$.

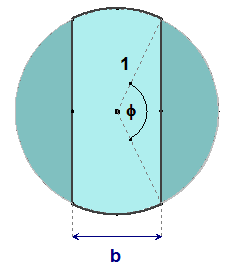
4. Na obrázku vidíte zvyšok kruhu s polomerom 1 po odstránení dvoch súmerných kruhových odsekov. Vyjadrite obsah tohto zvyšku

   • Najprv pomocou veľkosti stredového uhla $\varphi$

   • Potom pomocou hrúbky $\bf{b}$ zvyšku kruhu.

   Pozri tiež Podložka