MATEMATICKÁ ČÍTANKA

Obsah

2.1 Premenná

Príklad 9.

V mestskom divadle je spolu $\bf{800}$ miest. Existuje $\bf{5}$ druhov miest a teda $\bf{5}$ rôznych cien lístkov. Najdrahšie lístky sú druhu $\bf{A}$, cena lístka každého ďalšieho druhu je vždy o $\bf{100 \; SK}$ nižšia. Úhrnné ceny v jednotlivých druhoch miest udáva druhý riadok tabuľky. Zostavte rovnicu, z ktorej vypočítate aké sú ceny lístkov v jednotlivých kategóriách.

$$\begin{array}{|c|c|c|c|} \hline Druh & \bf{A} & \bf{B} & \bf{C} & \bf{D} & \bf{E} \\ \hline Úhrnná \; cena \; lístkov \; v \; Sk & \bf{16 800} & \bf{75 650} & \bf{104 000} & \bf{33 750} & \bf{15 000} \\ \hline Cena \; lístku & \bf{x + 200} & \bf{x + 100} & \bf{x} & \bf{x - 100} & \bf{x - 200} \\ \hline Počet \; miest \; daného \; druhu & \bf{\frac{16 800}{x + 200}} & \bf{\frac{75 650}{x + 100}} & \bf{\frac{104 000}{x}} & \bf{\frac{33 750}{x - 100}} & \bf{\frac{15 000}{x - 200}} \\ \hline \end{array}$$

Riešenie

Doplnili sme tabuľku o riadok, v ktorom sú neznáme ceny lístkov a o riadok, v ktorom uvádzame počet predaných lístkov. Zostavíme rovnicu pre počet miest: $$\bf{\bbox[yellow, 5px]{\frac{15000}{x - 200} + \frac{33750}{x - 100} + \frac{104000}{x} + \frac{75650}{x + 100} + \frac{16800}{x + 200} = 800 } }$$


Úlohy

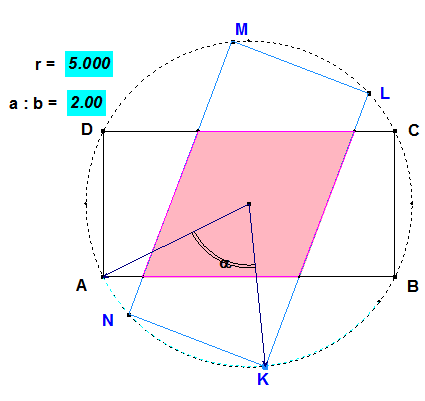
  1. Prémia! Do kružnice s polomerom $5$ je vpísaný obdĺžnik $\bf{ABCD}$, jeho strany sú v pomere $\bf{2 : 1}$. Jeho otočením okolo stredu $\bf{S}$ o uhol $\bf{\alpha}$ vznikol obdĺžnik $\bf{KLMN}$.

    Pozrite si Ot4u
    Vyjadrite pomocou premennej $\bf{\alpha}$ obsah prieniku a obsah zjednotenia obdĺžnikov $\bf{ABCD}$ a $\bf{KLMN}$. Za obor premennej $\bf{\alpha}$ zvoľte interval $\bf{(0^\circ; 90^\circ)}$.
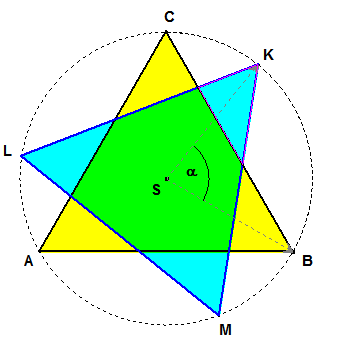
    obrazky

  2. Máme rovnostranný trojuholník $\bf{ABC}$ s obsahom $\bf{30 \; cm^2}$. Jeho otočením okolo stredu $\bf{S}$ o uhol $\bf{\alpha}$ vznikol trojuholník $\bf{KLM}$.

    Pozrite si Ot3u
    Vyjadrite pomocou premennej $\bf{\alpha}$ pomer obsahu prieniku trojuholníkov $\bf{ABC}$ a $\bf{KLM}$ ku obsahu trojuholníka $\bf{ABC}$. Za obor premennej zvoľte interval $\bf{(0^\circ; 120^\circ)}$.

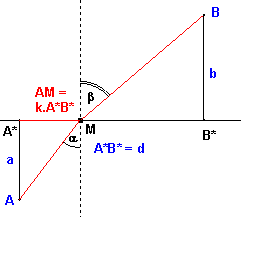
    obrazky

  3. Pomocou premennej $\bf{k \in (0; 1)}$ a parametrov $\bf{a, b, d, v_a , v_b}$ vyjadrite:

    • súčet vzdialeností $\bf{s(k) = |AM| + |MB|}$

    • čas potrebný na prejdenie dráhy z bodu $\bf{A}$ do bodu $\bf{M}$ rýchlosťou $\bf{v_a}$ a potom z bodu $\bf{M}$ do bodu $\bf{B}$ rýchlosťou $\bf{v_b}$.

    • pomer $\bf{\frac{\sin \alpha}{\sin \beta} }$

    obrazky

  4. Pán Konček spotreboval za roky $\bf{2002, 2003}$ a $\bf{2004}$ spolu $\bf{5000 \; m^3}$ zemného plynu. V uvedené roky platil za plyn $\bf{13\,880 \; Sk, 15\,143 \; Sk}$ a $\bf{16\,710 \; Sk}$. Zostavte rovnicu, z ktorej určíte ceny za $\bf{1 \; m^3}$ a spotrebu plynu v týchto rokoch ak viete, že v roku $\bf{2003}$ sa cena za $\bf{1 \; m^3}$ plynu zvýšila o $\bf{1.5 \; Sk}$ a v roku $\bf{2004}$ o ďalších $\bf{0.5 \; Sk}$. (Dobrá rada, za neznámu si zvoľte cenu plynu v r. $\bf{2003}$.)

Na záver ukážka toho, že vyjadrenie jednej veličiny pomocou druhej nás niekedy donúti zmobilizovať poznatky z rôznych častí matematiky:

Príklad 10.

Prúžok papiera šírky $\bf{p}$ preložíme pozdĺž úsečky $\bf{DE}$ tak, aby bod $\bf{B}$ prešiel do bodu $\bf{C}$. Vyjadrite dĺžku $\bf{d}$ záhybu len pomocou uhlu $\bf{\alpha}$.

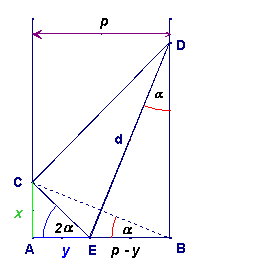
obrazky

Riešenie:

Uhly $\bf{\angle \, BAC}$ a $\bf{\angle \, DBE}$ sú zhodné, lebo sú to uhly s ramenami na seba kolmými. Uhol $\bf{\angle \, AEC}$ má veľkosť $\bf{2 \alpha}$, lebo trojuholník $\bf{BCE}$ je rovnoramenný. Zrejme platia vzťahy: $$\bf{d = \frac{p - y}{\sin \alpha}, \; y = \frac{x}{\tan 2 \alpha}, \; x = p \cdot \tan \alpha}, $$ ak si uvedomíme, že $$\bf{\tan 2 \alpha = \frac{2 \cdot \tan \alpha}{1 - \tan^2 \alpha}}$$ tak postupným dosadzovaním dostaneme: $$\bf{d(\alpha) = \frac{p}{2 \cdot \sin \alpha \cdot \cos^2 \alpha} }$$

Na záver uvedieme jeden problém pre čitateľov.

Problém

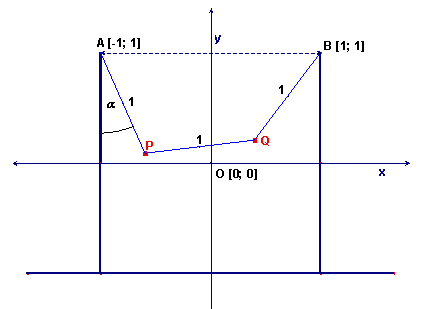
Dobre si všimnite obrázok a vyjadrite súradnice bodov $\bf{P, Q}$ pomocou uhla $\bf{\alpha}$.

obrazky