2.1 Premenná
Ďalšou oblasťou kde je rozhodujúcou schopnosť „vhodne“ zvoliť premennú sú problémy, ktoré vedú k vyriešeniu nejakej rovnice. V školskej matematike tomu hovorievame „slovné úlohy“.
Príklad 5.
Na obrázku vpravo je „kríž“ vpísaný do jednotkovej kružnice. Kríž je zjednotením obdĺžnika s jeho obrazom v otočení o 90°.
-
Vyjadrite obsah kríža pomocou premennej $\bf{x}$ resp $\bf{\alpha}$.
-
Nájdite takú hodnotu premenných $\bf{x}$ resp. $\bf{\alpha}$, pre ktorú je obsah kríža rovný polovici obsahu kruhu.

Riešenie
-
Ak použijeme ako premennú polovičnú šírku $\bf{x}$ vpísaných obdĺžnikov a označíme polovicu druhého rozmeru týchto obdĺžnikov ako $\bf{y}$, dostávame: $\bf{x^2 + y^2 = 1 \Rightarrow \bbox[yellow, 5px]{P(x)} = 2x \cdot 2y + 2x \cdot 2y - 2x \cdot 2x =}$ $\bf{4x(2y - x) = \bbox[yellow, 5px]{4x(2\sqrt{1 - x^2} - x)} }$
Ak použijeme ako premennú uhol $\bf{\alpha}$ dostávame : $\bf{x = \sin \alpha, \; y = \cos \alpha \Rightarrow \bbox[yellow, 5px]{P(\alpha) = 4 \cdot sin \alpha (2 \cdot \cos \alpha - \sin \alpha)} }$
-
Príslušné hodnoty premenných $\bf{x}$ resp. $\bf{\alpha}$ sú riešeniami rovníc [4]: $$\bf{\bbox[cyan, 5px]{4x(2\sqrt{1 - x^2} - x) \frac{\pi}{2} }, \; resp. \bbox[yellow, 5px]{4 \cdot \sin \alpha (2 \cdot \alpha - \sin \alpha) = \frac{\pi}{2} } }$$
Treba konštatovať, že zo zadania je zrejme $\bf{x \in (0; 1), \alpha \in (0; \frac{\pi}{2})}$
Mnohokrát je súčasťou úlohy niekoľko „parametrov“, t. j. veličín, ktoré sú z hľadiska riešenia problému konštantné, ale ktorých konkrétna hodnota ovplyvňuje kvalitu riešenia, alebo aj spôsob riešenia.
Príklad 6.
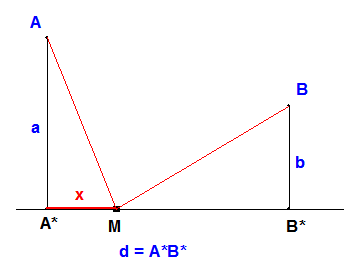
Vyjadrite pomocou premennej $\bf{x}$ a parametrov $\bf{a, b, d}$ súčet vzdialeností: $$\bf{s(x) = |AM| + |MB|}$$
Riešenie
Bezprostredne z Pytagorovej vety dostávame $$\bf{s(x) = \bbox[yellow, 5px]{\sqrt{x^2 + a^2} + \sqrt{(d - x)^2 + b^2} }}$$
Treba si uvedomiť, že parametre $\bf{a, b, d}$ môžu nadobúdať ľubovoľnú kladnú hodnotu a ak predpokladáme že bod $\bf{M}$ je bodom úsečky $\bf{A*B*}$, tak oborom premennej $\bf{x}$ je interval $\bf{(0 ; d)}$.
Príklad 7.
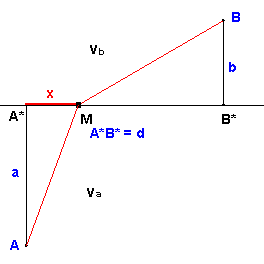
Pomocou premennej $\bf{x}$ a parametrov $\bf{a, b, d}$ vyjadrite čas potrebný na prejdenie dráhy z bodu $\bf{A}$ do bodu $\bf{M}$ rýchlosťou $\bf{v_a}$ a potom z bodu $\bf{M}$ do bodu $\bf{B}$ rýchlosťou $\bf{v_b}$.
Riešenie
Z Pytagorovej vety a z vlastností rovnomerného priamočiareho pohybu dostávame: $$\bf{t(x) = \bbox[yellow, 5px]{\frac{\sqrt{x^2 + a^2}}{v_a} + \frac{\sqrt{(d - x)^2} + b^2}{v_b}}}$$ oborom premennej $\bf{x}$ je interval $\bf{0; d}$
Príklad 8.
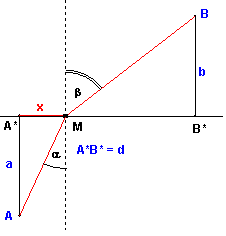
Zostavte rovnicu, z ktorej vypočítate pre ktorú hodnotu premennej $x$ bude platiť $$\bf{\sin \alpha : \sin \beta = 1 : 2}$$
Riešenie
Máme nájsť také $x$, pre ktoré je $\bf{\sin \beta = 2 \cdot \sin \alpha}$
Z Pytagorovej vety a zo zhodnosti striedavých uhlov dostávame: $$\bf{\frac{d - x}{\sqrt{(d - x)^2 + b^2}} = 2 \cdot \frac{x}{\sqrt{x^2 + a^2}}}$$ oborom premennej $\bf{x}$ je interval $\bf{0; d}$.