4.2 Rozprávka o čísle e
Príklad 1.
Pomocou (D) dokážeme, že z prvej rovnosti v (exp) vyplýva prvá rovnosť v (ln).
Podľa (D) $\bf{ln(u \cdot v) = ln(u) + ln(v) \iff e^{ln(u) + ln(v)} = u \cdot v }$. Vďaka (exp) môžeme písať: $\bf{e^{ln(u)+ln(v)} = e^{ln(u)} \cdot e^{ln(v)}}$ čo sa podľa (D) rovná $\bf{u \cdot v}$.
Úlohy
-
Podobne ako v predchádzajúcom príklade dokážte druhú rovnosť vo vzťahu (ln).
-
Ktorá funkcia je inverzná k funkcii $\bf{y = \sqrt{x}}$?
-
Ktorá funkcia je inverzná k funkcii $\bf{y = 3x + 2}$?
(pozrite si INV1)
-
Ktorá funkcia je inverzná k funkcii $\bf{y = \frac{2x-1}{x+2} }$?
(pozrite si INV2)
-
Prémia. Na obrázku vidíte priesečník grafov funkcií $\bf{y = ln(x)}$ a $\bf{y = (1-x)^{0.3}}$.
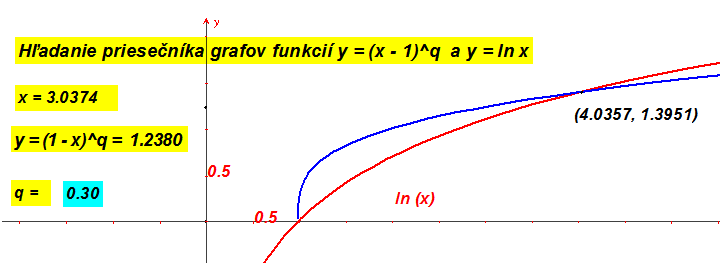
Otvorte si Cabri výkres Exp04 a pokúste sa vysloviť hypotézu pre ktoré $\bf{q\in (0;1)}$ majú grafy funkcií $\bf{y = ln(x)}$ a $\bf{y = (1-x)^q}$ spoločný bod rôzny od bodu $[1;0]$.
Exp04
Poznámka historická
Keď autor tejto čítanky chodil do strednej školy, boli schopnosti narábať s logaritmami, s logaritmickými tabuľkami a s logaritmickým pravítkom kľúčovými schopnosťami a ich neznalosť sa netolerovala. Dôležité bolo napr. poznať vzťah medzi logaritmami pri rôznych základoch a schopnosť riešiť špeciálne zostavené exponenciálne a logaritmické rovnice. Nebudeme pokračovať v takejto drezúre, ale uvedieme niekoľko príkladov a úloh, ktoré nás donútia zamyslieť sa nad exponenciálnymi a logaritmickými funkciami.
Príklad 2.
Určte bez použitia funkcie $\bf{y = ln(x)}$ hodnotu $\bf{ln(2)}$ s presnosťou na $8$ desatinných miest.
Prvý odhad získame pohľadom na funkciu $\bf{y = (1,001^{1000})^x}$ v zošite e04 . Tam vidíme: \begin{array}{:c:c:}\hdashline 0,693 & 1,9990133 &\color{gray} 1,99901334398633\\ \hdashline 0,694 & 2,0010124 & \color{gray} 2,00101235733032 \\ \hdashline \end{array}
Čiže $\bf{ln(2)}$ je medzi $\bf{0,693}$ a $\bf{0,694}$. Zjemnenie kroku na $\bf{0,0001}$ dá odhad: \begin{array}{:c:c:}\hdashline 0,6931 & 1,99983634 &\color{gray} 1,99983634019676\\ \hdashline 0,6932 & 2,00003632 & \color{gray} 2,00003632383078 \\ \hdashline \end{array}
Čiže $\bf{ln(2)}$ je medzi $\bf{0,6931}$ a $\bf{0,6932}$.
Lepšie bude použiť postup podobný pri odhade $\bf{\sqrt{2}}$. Pozrite si 2. hárok zošitu e04 . Postupným zjemňovaním kroku dostávame približný odhad: $\bf{ln(2) ≈ 0,69314718}$.