MATEMATICKÁ ČÍTANKA

Príklad 3.

Vypočítajte približný obsah útvaru ohraničeného osou $\bf{x}$, priamkami $\bf{x = 1}$ a $\bf{x = 2}$ a grafom funkcie $\bf{y = \frac{1}{x}}$. (Pozri obrázok.)

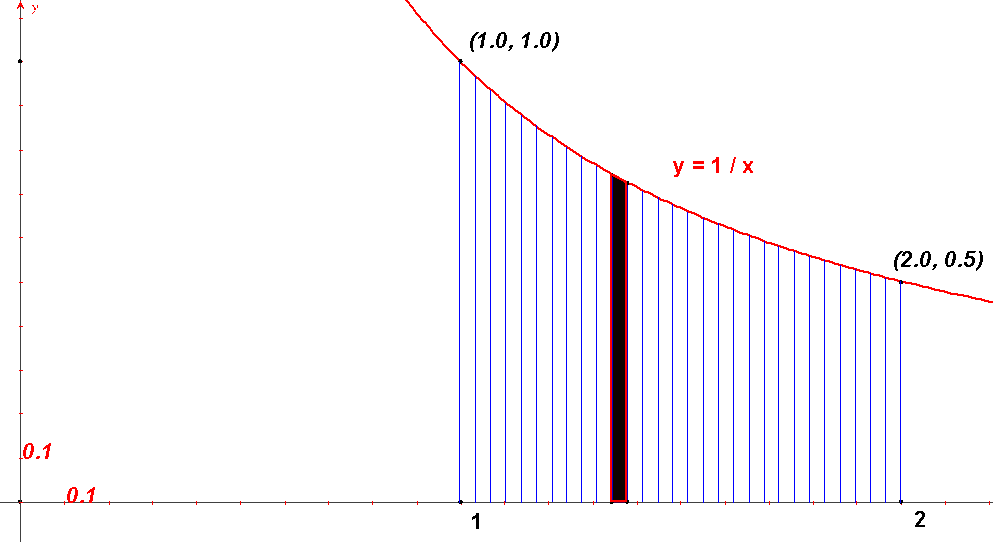
Samotný obrázok navádza na riešenie. Približnú hodnotu obsahu vyšrafovanej oblasti získame ako súčet obsahov $\bf{n}$ vpísaných lichobežníkov s rovnakou výškou $\bf{\frac{1}{n}}$. Deliace body na osi $x$ sú čísla $\bf{1 + \frac{i}{n}=\frac{n+i}{n}}$, kde $\bf{i \in \{0,1,2,...,n-1,n\}}$. Funkčné hodnoty v týchto bodoch, t. j. čísla $\bf{z_i = \frac{n}{n+i}}$ sú základňami týchto lichobežníkov. Podľa vzorca pre obsah i - teho lichobežníka $\bf{P_i = (z_{i-1}+z_i)\cdot \frac{v}{2}}$ pre súčet obsahov týchto n lichobežníkov platí: $$\bf{P(n) = \sum_{i=1}^nP_i = [(z_0+z_1)+(z_1+z_2)+...+(z_{n-2}+z_{n-1})+(z_{n-1}+z_n)]\frac{v}{2}} =$$ $$\bf{= (\frac{n}{n}+\frac{2n}{n+1}+\frac{2n}{n+2}+...+\frac{2n}{n+n-1}+\frac{n}{2n})\frac{1}{2n} = }$$ $$\bf{= \bbox[yellow,3px]{\frac{1}{4n}+\frac{1}{n+1}+\frac{1}{n+2}+...+\frac{1}{2n-1}+\frac{1}{2n}}}$$

Myslím si, že snaha „upraviť“ žltý výraz sčítaním zlomkov, aby sme dostali explicitný vzorec pre výpočet $\bf{P(n)}$, je nezmyselná. Rozumnejšie bude nájsť vzťah, ktorý zo známeho $\bf{P(n)}$ nám umožní vypočítať $\bf{P(n+1)}$. Ak si vyjadríme $\bf{P(n)}$ pre prvých pár $\bf{n}$ dostávame: \begin{array}{cc} \bf{P(1)= \frac{1}{4}+\frac{1}{2}} & \bf{P(2)= \frac{1}{8}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}} & \bf{P(3)= \frac{1}{12}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}} & \bf{P(1)= \frac{1}{16}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}} \end{array}

Z toho sa už dá usúdiť, že: $$\bf{\bbox[cyan, 3px]{P(n+1) = P(n) - \frac{1}{4n} - \frac{1}{n+1}+\frac{1}{4n+4}+\frac{1}{2n+1}+\frac{1}{2n+2}}}$$

Tento vzťah sa pokúsime zužitkovať pri výpočte v zošite ln(2) . Vypočítali sme $\bf{P(n)}$ pre $\bf{n}$ od $\bf{1}$ do $\bf{1000}$. Porovnanie posledných dvoch hodnôt: \begin{array}{:c:c:}\hdashline \bbox[cyan, 3px]{1999} & \bbox[cyan, 3px]{0,6931471962} \\ \hdashline \bbox[cyan, 3px]{2000} & \bbox[cyan, 3px]{0,6931471962}\\ \hdashline \end{array}

S výsledkom príkladu 2: $\bf{ln(2)≈ 0,69314718}$