4.2 Rozprávka o čísle e
Poznámka 1.
Ako žiak strednej školy som nerozumel tomu prečo sa číslo $\bf{e}$ volá základ prirodzených logaritmov.
Čo už je na tomto ani nie algebrickom čísle prirodzené? Zdá sa, že odpoveď je jednoduchá. Hore uvedené
vhodné základy tvoria členy postupnosti, ktorá konverguje k číslu $\bf{e \sim 2,7182818...}$
(Pozri e03, podrobnejšie sa o tejto postupnosti dozviete v kapitole „Limitné procesy“.)
Takže číslo $\bf{e}$ je preto „prirodzené“, že jeho približné hodnoty, t. j. čísla $\bf{a_n}$ sú mimoriadne vhodné ako základ pri tvorbe tabuliek exponenciálnej funkcie s krokom $\bf{10^{– n}}$.
Aby aj táto rozprávka mala šťastný koniec, urobme si tabuľky funkcie: $\bf{y = (1,001^{1000})^x}$ pre $\bf{x}$ z intervalu $\bf{\langle 0; 1 \rangle}$ s krokom $\bf{0,001}$.
Pri ich výrobe sme použili EXCEL, celé sú v zošite e04 . , tu uvádzame len prvých 20 a posledných 10 hodnôt.
V 1. stĺpci sú hodnoty premennej $\bf{x}$ od $\bf{0}$ po $\bf{1}$ s krokom $\bf{0,001}$.
3. stĺpec začína číslom $1$ a každá ďalšia hodnota je rovná predchádzajúcej vynásobenej číslom $\bf{1,001}$.
2. vznikol z 3. stĺpca zaokrúhlením na $\bf{7}$ desatinných miest.
\begin{array}{:c:c:}\hdashline n = & 3 \\\hdashline step = & 0,001 \\\hdashline base = & 1,001 \\\hdashline 0 & 1 &\color{gray} 1,00000000000000\\\hdashline 0,001 & 1,001 &\color{gray} 1,00100000000000\\\hdashline 0,002 & 1,002001 &\color{gray} 1,00200100000000\\\hdashline 0,003 & 1,003003 &\color{gray} 1,00300300100000\\\hdashline 0,004 & 1,004006 &\color{gray} 1,00400600400100\\\hdashline 0,005 & 1,00501 &\color{gray} 1,00501001000500\\\hdashline 0,006 & 1,006015 &\color{gray} 1,00601502001501\\\hdashline 0,007 & 1,007021 &\color{gray} 1,00702103503502\\\hdashline 0,008 & 1,0080281 &\color{gray} 1,00802805607005\\\hdashline 0,009 & 1,0090361 &\color{gray} 1,00903608412612\\\hdashline 0,010 & 1,0100451 &\color{gray} 1,01004512021025\\\hdashline 0,011 & 1,0110552 &\color{gray} 1,01105516533046\\\hdashline 0,012 & 1,0120662 &\color{gray} 1,01206622049579\\\hdashline 0,013 & 1,0130783 &\color{gray} 1,01307828671629\\\hdashline 0,014 & 1,0140914 &\color{gray} 1,01409136500300\\\hdashline 0,015 & 1,0151055 & \color{gray} 1,01510545636801 \\\hdashline 0,016 & 1,0161206 & \color{gray} 1,01612056182437 \\\hdashline 0,017 & 1,0171367 & \color{gray} 1,01713668238620 \\\hdashline 0,018 & 1,0181538 & \color{gray} 1,01815381906858 \\\hdashline 0,019 & 1,019172 & \color{gray} 1,01917197288765 \\\hdashline 0,020 & 1,0201911 & \color{gray} 1,02019114486054 \\\hdashline \end{array} \begin{array}{:c:c:} 0,99 & 2,6899035 & \color{gray} 2,68990352794343 0,991 & 2,6925934 & \color{gray} 2,69259343147137 0,992 & 2,695286 & \color{gray} 2,69528602490284 0,993 & 2,6979813 & \color{gray} 2,69798131092774 0,994 & 2,7006793 & \color{gray} 2,70067929223867 0,995 & 2,70338 & \color{gray} 2,70337997153091 0,996 & 2,7060834 & \color{gray} 2,70608335150244 0,997 & 2,7087894 & \color{gray} 2,70878943485394 0,998 & 2,7114982 & \color{gray} 2,71149822428880 0,999 & 2,7142097 & \color{gray} 2,71420972251309 1 & 2,7169239 & \color{gray} 2,71692393223560 \end{array}V zošite e04 . je viac než len popísané tabuľky. Nie je tam totiž funkcia $\bf{y = (1,001^{1000})^x }$, ale $$\bf{\bbox[yellow, 3px]{y = (1+10^{-n})^{(10)^n}}}$$ pričom $\bf{n}$ si môžete ľubovoľne meniť. Ak však zvolíte $\bf{n \gt 3}$, budete si musieť tabuľku rozšíriť o ďalšie riadky.
Poznámka 2.
Toto bola len rozprávka. Takto mohli vzniknúť tabuľky exponenciálnych funkcií. Tieto by však mali pri praktickom používaní jednu chybu. Ak si znovu pozriete 1. obr. v tejto kapitole, vidíte, že pri nahradení násobenia dvoch čísel (pomocou tabuliek exponenciálnej funkcie) sčitovaním by sme museli dvakrát použiť tabuľky v „opačnom“ smere (t. j. od y ku x) a len raz priamo (od x ku y).
Keby sme napr. mali vypočítať $\bf{1,004 \cdot 1,007}$ tak zistíte, že tieto čísla sa v 2. stĺpci tabuľky nenachádzajú, museli by ste používať tzv. lineárnu interpoláciu t. j. nahradenie funkcie medzi dvoma tabelovanými hodnotami lineárnou funkciou. Proste, tabuľky sa pohodlne používajú v smere od x ku y a výrazne menej pohodlne v smere opačnom. Preto sa pre praktické výpočty používali tabuľky funkcie, ktorá je ku exponenciálnej inverzná - tabuľky logaritmickej funkcie. Situáciu Vám môže priblížiť obrázok:
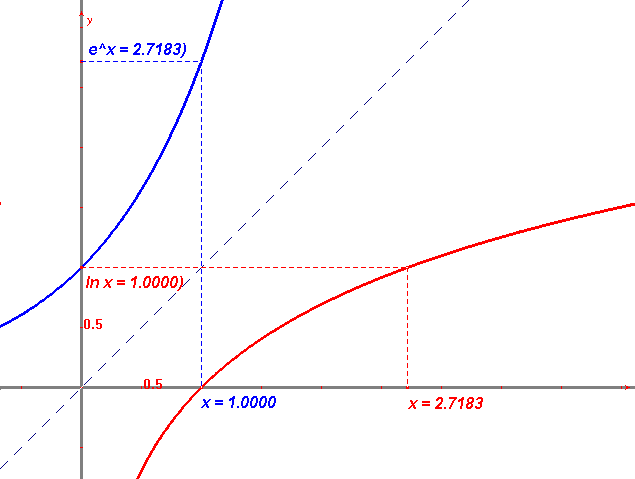
Resp., jeho „živá“ podoba exp03.
Inak povedané platí: $$\bf{\forall u \in R^+, \; \forall a \in R: ln u = a \iff e^a = u \qquad (D)}$$ Preto z vlastností exponenciálnej funkcie: $$\bf{\forall a,b \in R: e^{a+b} = e^a \cdot e^b,\; \forall a \in R \; \forall p \in R: (e^a)^p = e^{a \cdot p} \qquad (exp) }$$ Vyplývajú vlastnosti logaritmickej funkcie: $$\bf{\forall u,v \in R^+, \; \forall p \in R: ln(u\cdot v) = ln(u)+ln(v),\; ln(u^p)=p\cdot ln(u) \qquad (ln)}$$
Funkcia inverzná k funkcii $\bf{y = g^x}$ sa volá logaritmus pri základe g, špeciálne pre $\bf{g = 10}$ máme „dekadický“ logaritmus. Označujeme ho $\bf{y = log_{10}(x)}$.