4.2 Rozprávka o čísle e
Príklad 4.
Zamyslime sa nad otázkou: Ktorý z dvoch „krivočiarych lichobežníkov“ má väčší obsah, modrý, alebo zelený?
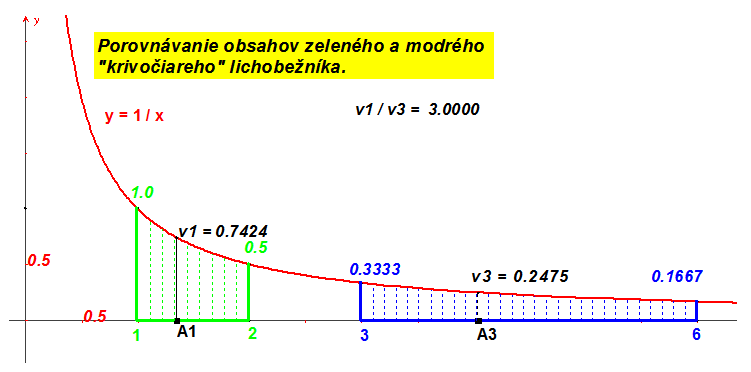
Modrý má trikrát väčší vodorovný rozmer, ale v ľubovoľnom bode je jeho zvislý rozmer trikrát menší.
Otvorte si cabri výkres Ln a pohybujte s bodom A1.
To nás oprávňuje vysloviť tvrdenie, že obsahy týchto útvarov sú rovnaké. Toto tvrdenie by sa dalo zovšeobecniť. Ak by sme obsah útvaru ohraničeného osou $\bf{x}$, grafom funkcie $\bf{y = \frac{1}{x}}$ a priamkami $\bf{x = a, x = b}$ označili symbolom $\bf{P_a^b}$, tak by platilo: $\bf{P_1^a = P_a^{ab}}$.
Môžeme to chápať aj ako funkciu. Obsah útvaru ohraničeného osou $\bf{x}$, grafom funkcie $\bf{y = \frac{1}{x} $ a priamkami $\bf{x = 1, x = a}$ môžeme označiť ako $\bf{F(a)}$.
Táto funkcia má zaujímavú vlastnosť: $\bf{\bbox[yellow, 3px]{F(a)+ F(b)} = P_1^a + P_1^b = P_1^b + P_b^{ab} = \bbox[yellow, 3px]{F(ab)} }$
Nepripomína Vám to vlastnosť: $\bf{\forall u,v \in R^+: ln(u\cdot v) = ln(u) + ln(v)}$?
Úlohy
-
Vypočítajte (podobne ako v príklade 3.) približný obsah útvaru ohraničeného osou $\bf{x}$, priamkami $\bf{x = 1}$ a $\bf{x = 3}$ a grafom funkcie $\bf{y = \frac{1}{x}}$.
Poznámka záverečná.
Číslo $\bf{e}$, základ prirodzených logaritmov má v matematike významné miesto. V kapitole o limitných procesoch a v ďalších v druhej knihe, ukážeme viacero procesov, ktorých výsledok speje k tejto konštante.