MATEMATICKÁ ČÍTANKA

Analogické úlohy získame, ak budeme „algebraizovať“ niektoré úlohy o lineárnych útvaroch v priestore:

Príklad 2.

Nech usporiadané trojice $\bf{(-2; 3; 4), \; (4; -1; 2)}$ a $\bf{(1; 2; -1)}$ sú riešeniami nejakej lineárnej rovnice s troma neznámymi.

1. Nájdite aspoň dve ďalšie trojice, ktoré sú riešeniami tejto rovnice

2. Určte túto rovnicu

3. Nájdite všetky riešenia tejto rovnice a zapíšte ich „jedným vrzom“ s použitím dvoch parametrov.

Pokúsili sme sa nakresliť celú situáciu na obr. 3D súr.

3D súr

ale situácia je málo prehľadná, obrázok neposkytuje nápad na okamžité riešenie úlohy. Skúsme preto rýdzo algebricky vyriešiť problém $\bf{b}$.

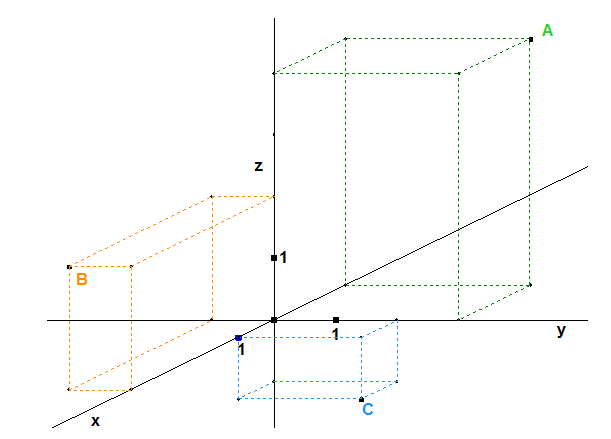
Hľadáme také čísla $\bf{a, b, c, d}$, aby usporiadané trojice $\bf{(-2; 3; 4), (4; -1; 2)}$ a $\bf{(1; 2; -1)}$ boli riešeniami rovnice $\bf{ax + by + cz + d = 0}$.

To ale znamená, že má platiť: $$\begin{align} \bf{-2 \cdot a + 3 \cdot b + 4 \cdot c + d = 0} \\ \bf{4 \cdot a - 1 \cdot b + 2 \cdot c + d = 0} \\ \bf{1 \cdot a + 2 \cdot b - 1 \cdot c + d = 0} \\ \end{align}$$

Sústavu sme vyriešili v 1. hárku zošitu Rovnica. Riešením je rovnica $\bf{\bbox[yellow, 3px]{{3x + 4y + 1z – 10 = 0}}$.

1. hárok zošitu Rovnica

Teraz ľahko vyriešime problém $\bf{c}$. a tým vlastne aj problém $\bf{a}$. Našu poslednú rovnicu proste vyriešime. Jednu neznámu vyjadríme pomocou zvyšných dvoch, (hodí sa na to $\bf{z}$) a zvyšné dve môžu nadobúdať ľubovoľné hodnoty, takže ak si zvolíme $\bf{x = u, \; y = v}$ dostávame: $$\begin{array}{rr} \bf{x =} & & \bf{u} \\ \bf{y =} & & & \bf{v} \\ \bf{z = } & \bf{10} & \bf{-3u} & \bf{-4v} \\ \end{array}$$

Poznámka

Rovnakým spôsobom sme mohli vyriešiť problém $\bf{c.}$ aj v 1. príklade. Skúsme to:

Hľadáme rovnicu typu: $\bf{ax + by +c = 0}$, ktorej riešeniami sú dvojice $\bf{(-1; \; 1)}$ a $\bf{(2; \; 2)}$.

To znamená, že platí: $$\begin{array}{:c:c:} \hdashline \bbox[yellow, 3px]{\bf{-a}} & \bbox[yellow, 3px]{\bf{+}} & \bbox[yellow, 3px]{\bf{b}} & \bbox[yellow, 3px]{\bf{+}} & \bbox[yellow, 3px]{\bf{c}} & \bbox[yellow, 3px]{\bf{=}} & \bbox[yellow, 3px]{\bf{0}}\\ \hdashline \bbox[yellow, 3px]{\bf{2a}} & \bbox[yellow, 3px]{\bf{+}} & \bbox[yellow, 3px]{\bf{2b}} & \bbox[yellow, 3px]{\bf{+}} & \bbox[yellow, 3px]{\bf{c}} & \bbox[yellow, 3px]{\bf{=}} & \bbox[yellow, 3px]{\bf{0}}\\ \hdashline \end{array}$$

Schopnosť vedieť vyriešiť sústavu dvoch homogénnych lineárnych rovníc o troch neznámych budeme potrebovať viackrát (v Geometrii pri premene parametrických rovníc roviny na všeobecnú rovnicu, pri určovaní vektorového súčinu). Venujme preto trochu času riešeniu sústavy: $$\begin{array}{:c:c:} \hdashline\bf{a_1x} & \bf{+} & \bf{b_1y} & \bf{+} & \bf{c_1z} & \bf{=} & \bf{0} \\ \hdashline\bf{a_2x} & \bf{+} & \bf{b_2y} & \bf{+} & \bf{c_2z} & \bf{=} & \bf{0} \\ \hdashline \end{array}$$

Použijeme osvedčenú metódu „spadlo z neba“ (propagátorom a autorom názvu je G. Pólya) a uvedieme jedno riešenie. Je ním trojica $\bf{(b_1c_2 – b_2c_1; \; c_1a_2 – c_2a_1; a_1b_2 – a_2b_1)}$. Všetky ostatné riešenia sú jej násobkom. Vhodnou mnemotechnickou pomôckou na získanie tohto riešenia je tabuľka: $$\begin{array}{:c|c:c:} \hdashline\bf{a_1} & \bf{b_1} & \bf{c_1} & \bf{a_1} & \bf{b_1} \\ \hdashline\bf{a_2} & \bf{b_2} & \bf{c_2} & \bf{a_2} & \bf{b_2} \\ \hdashline & & \bbox[yellow, 3px]{ \bf{b_1c_2 - b2_c1}} & \bbox[yellow, 3px]{ \bf{c_1a_2 - c2_a1}} & \bbox[yellow, 3px]{ \bf{a_1b_2 - a2_b1}} \\ \hdashline \end{array}$$

Podľa tejto schémy pre náš príklad dostávame: $$\begin{array}{:c|c:c:} \hdashline\bf{-1} & \bf{1} & \bf{1} & \bf{-1} & \bf{1} \\ \hdashline\bf{2} & \bf{2} & \bf{1} & \bf{2} & \bf{2} \\ \hdashline & & \bbox[yellow, 3px]{ \bf{-1}} & \bbox[yellow, 3px]{ \bf{3}} & \bbox[yellow, 3px]{ \bf{-4}} \\ \hdashline \end{array}$$

Teda hľadanou rovnicou je napr. rovnica $\bf{-x + 3y = 4}$

V zošite Rovnice 2 v 1. liste nájdete tento recept, a v 2. liste klasické riešenie sústavy rovníc pomocou úprav matice.