Goniometrické funkcie
Dúfam že už lepšie rozumiete prečo má orientovaný uhol nekonečne veľa veľkostí a viete aký je medzi nimi vzťah. Takže môžete vyriešiť
Úlohy
-
Doplňte text: Reálne čísla $\bf{a, b}$ sú veľkosťami toho istého orientovaného uhla práve vtedy keď .......................... .
V nasledujúcom príklade si chceme názorne priblížiť čo to je „sčitovanie orientovaných uhlov“.
Príklad 2.
Definujme „sčitovanie“ bodov kružnice takto (pozri obrázok): Nech $\bf{O}$ je pevný bod kružnice, „súčtom“ $\bf{A + B}$ bude taký bod $\bf{C}$, pre ktorý platí, že osi oblúkov $\bf{AB}$ a $\bf{OC}$ sú totožné.
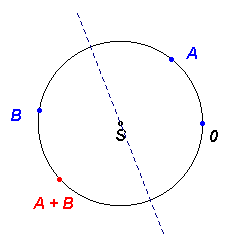
Toto sčitovanie je zrejme komutatívna operácia, asociatívna je tiež, i keď to už nie je tak samozrejmé.
Ak si pozriete výkres suma uhlov, môžete si sami zistiť, čo je „nulou“ pri tomto sčitovaní a ako
geometricky súvisia body $\bf{A}$ a $\bf{- A}$.
suma uhlov
Poznámka pre učiteľov
Množina bodov kružnice s takto definovanou operáciou je komutatívna grupa, ktorá má podobné vlastnosti ako sčitovanie reálnych čísel, ale má aj pozoruhodné odlišnosti, ako ukazuje nasledovný príklad:
Príklad 3.
Pozrite si obrázok vpravo a nájdite všetky také body $\bf{X, Y, Z}$ na kružnici $\bf{k}$, pre ktoré platí: \begin{array}{cc} \bf{X+X=A \qquad(1),} & \bf{Y+Y+Y=B \qquad(2),} & \bf{Z+Z+Z+Z=C \qquad(3)} \end{array}
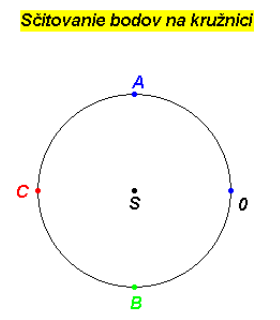
Riešenie
Rovnice (1) až (3) majú napodiv na rozdiel od rovnakých rovníc v množine reálnych čísel viacero riešení.
Skôr než si pozriete riešenie, skúste sami nájsť riešenie týchto rovníc pomocou cabri vo výkrese suma uhlov 2.
Na sérii troch obrázkov vidíte 2 riešenia rovnice (1), tri riešenia rovnice (2) a 4 riešenia rovnice (3).