MATEMATICKÁ ČÍTANKA

V predchádzajúcom príklade sme sa naučili ako reálnemu číslu $\bf{x}$ priradiť orientovaný uhol, ktorého jednou veľkosťou je práve toto číslo. Zužitkujme tieto poznatky o namotávaní na oživenie školskej definície goniometrických funkcií sínus a kosínus:

Dané číslo $\bf{x}$ zobrazíme na pomocnej číselnej osi (ležiacej na priamke $\bf{x = 1)}$

Toto číslo namotáme na jednotkovú kružnicu so stredom v začiatku súradnicovej sústavy.

Namotaný bod $\bf{X}$ leží na 2. ramene orientovaného uhla $\bf{1OX}$, ktorého jednou veľkosťou je číslo $\bf{x}$.

Namotaný bod $\bf{X}$ má súradnice $\bf{[\cos x; \sin x]}$.

Ilustráciu tejto definície, aj definície funkcie kosínus si môžete pozrieť na Cabri výkresoch:

Dúfam, že oba cabri výkresy vám pomohli porozumieť stredoškolskej definícii funkcií sínus a kosínus.

Poznámka 1.

Slová „toto číslo namotáme na jednotkovú kružnicu so stredom v začiatku súradnicovej sústavy“ sú rovnako presné, či rovnako nepresné ako slová „zostrojíme orientovaný uhol, ktorého jednou veľkosťou je dané číslo“. Korektná definícia goniometrických funkcií je možná len:

• pomocou ich funkcionálnych vlastností (pozri napr. Jarník: „Úvod do počtu diferenciálneho“). Túto možnosť využijeme v závere kapitoly na zostrojenie tabuliek funkcií sínus a kosínus,

• pomocou súčtu nekonečných radov: $$\bf{\cos x = 1 - \frac{x^2}{2!}+ \frac{x^4}{6!}-\frac{x^6}{6!}+...+(-1)^k \frac{x^{2k}}{(2k)!}} \qquad(c)$$ $$\bf{\sin x = x - \frac{x^3}{3!}+ \frac{x^5}{5!}-\frac{x^7}{7!}+...+(-1)^{k+1} \frac{x^{2k-1}}{(2k-1)!}} \qquad(s)$$

Ak v oboch radoch použijeme len niekoľko sčítancov, chyba o ktorú sa budeme líšiť od celkového súčtu bude menšia ako absolútna hodnota posledného použitého člena. To nám dáva návod, ako napr. s presnosťou na 5 desatinných miest ručne vypočítať: $$\bf{\sin 0.5 = \frac{1}{2}-\frac{1}{48}+\frac{1}{3840}-\frac{1}{645120} = \frac{322560-13440+168-1}{645120} = \frac{309287}{645120} ≈ 0.47943}$$

Poznámka 2.

Rovnosti (c) a (s) majú aj inú interpretáciu. Ak budeme postupne uvažovať funkcie: \begin{array}{ll} \bf{y = x} & & \text{na obr. modrá}\\ \bf{y = x - \frac{x^3}{3!}} & & \text{na obr. tyrkysová}\\ \bf{y = x - \frac{x^3}{3!} + \frac{x^5}{5!}} && \text{na obr. zelená}\\ \bf{y = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!}} && \text{na obr. červená} \end{array} ktoré získame, ak z radu (s) postupne použijeme čoraz viac členov, tieto budú v čoraz väčšej vzdialenosti od nuly dostatočne presne aproximovať funkciu $\bf{y = \sin x}$ (na obr. čierna).

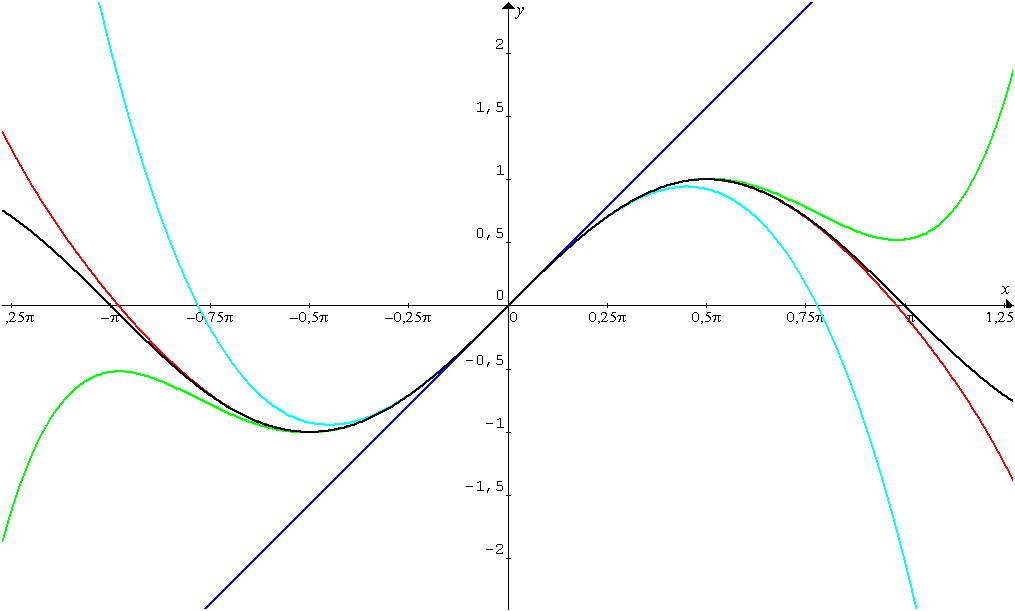
Podobný obrázok pre aproximáciu funkcie kosínus nájdete v Cabri výkrese kosínus.