MATEMATICKÁ ČÍTANKA

Funkcie inverzné ku goniometrickým funkciám

Spomínate si na dvojicu funkcií $\bf{y = e^x}$ a $\bf{y = ln x}$ z predchádzajúcej kapitoly? Podobne ako je logaritmická funkcia inverzná ku funkcii exponenciálnej, je možné vytvoriť aj funkcie inverzné ku funkciám sínus, kosínus a tangens.

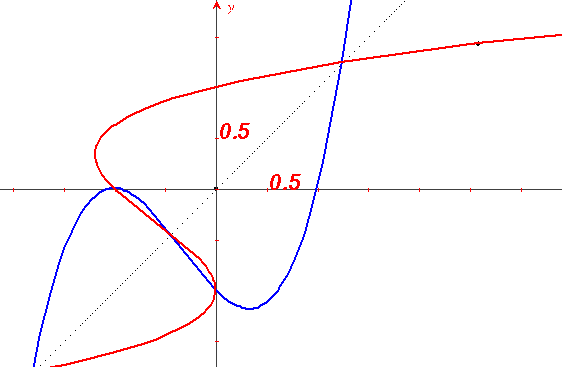
Musíme si však dať pozor. Na obrázku vidíte červený graf súmerný s modrým podľa osi 1. kvadrantu. Kým modrá krivka je grafom funkcie, červená nie je. (Lebo pre niektoré x nadobúda viacero hodnôt, čo je v rozpore s definíciou pojmu funkcia.) Preto inverzná funkcia bude existovať len k takej funkcii, ktorá nadobúda každú hodnotu najviac raz. Také funkcie sa volajú prosté. Ak funkcia nie je prostá, inverzná funkcia môže existovať len k takej jej časti, ktorá prostá je. Preto nebudeme robiť inverzné funkcie k celým funkciám sínus, kosínus a tangens, ale len k ich častiam.

Na obrázku vidíte graf funkcie inverznej k funkcii $\bf{\bbox[yellow, 3px]{y = \cos x, \; x \in \langle 0; \pi \rangle}}$.

Tento obrázok si môžete pozrieť v živej podobe vo výkrese Arccos. Grafy funkcie arkus sínus nájdete vo výkrese Arcsin a graf funkcie arkus tangens si urobte pomocou cabri sami.

Dodatok.

Tabuľky hodnôt goniometrických funkcií.

Definícia funkcií sínus a kosínus (pozri napr. Jarník: Úvod do počtu diferenciálního) neobsahuje návod, či algoritmus na výpočet ich hodnôt, iba ich funkcionálnu charakteristiku. Sínus a kosínus sú podľa tejto definície také spojité funkcie $\bf{f(x), g(x)}$, pre ktoré platí:

• $\bf{\forall a \in R: f(a+b) = f(a) \cdot g(b) + g(a) \cdot f(b) \; \land \; g(a+b)=g(a)\cdot g(b)-f(a)\cdot f(b)}$

• $\bf{f(0) = 0,\; g(0) = 1}$

• $\bf{\forall x \in R: g(x) = \sqrt{1-f^2(x)}}$

Dajú sa len z týchto vlastností vypočítať hodnoty týchto funkcií napr. v intervale $\bf{\langle 0; \frac{\pi}{4} \rangle}$?

Asi nerozumiete slovu „spojité“. Zatiaľ nám stačí, keď zmysel slov „spojitá funkcia“, budeme chápať tak, že to znamená, že malej zmene hodnoty premennej odpovedá malá zmena funkčnej hodnoty. Keďže $\bf{f(0) = 0}$, vyložíme si tento fakt tak, že aj pre dostatočné malé $\bf{\delta}$ bude platiť $\bf{f(\delta) ≈ \delta.

Naše tabuľky zhotovíme pre $\bf{x \in \langle 0; \frac{\pi}{4}\rangle}$, s krokom (stepom) $\delta = 1$ minúta. V radiánovej miere $\bf{\delta = 0.000290888}$. Budeme teda predpokladať, že: $$\bf{\sin (\delta) ≈ \delta = 0.000290888 \; a \; \cos(\delta) ≈ \sqrt{1-\delta^2} = 0.999999958 }$$ ak použijeme počiatočné podmienky $\bf{\sin 0 = 0 , \cos 0 = 1}$ a rekurentné vzťahy: $$\bf{\sin(x+\delta) = \sin x \cdot \sqrt{1-\delta^2} + \cos x \cdot \delta}$$ $$\bf{\cos(x+\delta) = \cos x \cdot \sqrt{1-\delta^2} - \sin x \cdot delta }$$ a budeme pokračovať až po $\bf{\frac{\pi}{4}}$ , dostaneme tabuľky funkcií sínus a kosínus .

Keď si otvoríte tento zošit, uvidíte že sme pre kontrolu v stĺpcoch G a H uviedli hodnoty týchto funkcií, ktoré ponúka EXCEL. Nami vypočítané hodnoty sme uviedli len na toľko desatinných miest, aby sa nelíšili od oficiálnych tabuliek.