Goniometrické funkcie
Poznámka o grafoch goniometrických funkcií
Už sme spomínali v kapitole o polynomických funkciách, že existujú viaceré matematické i didaktické softvéry, ktoré umožňujú presne a rýchlo nakresliť graf žiadanej funkcie. Pomocou Cabri však môžeme pochopiť podstatu pojmu funkcia a kresliť grafy parametrických súborov funkcií.
S pomocou ponúk „výraz“ a „použi výraz“ (ktorá sú súčasťou CABRI II plus) môžeme nakresliť graf ľubovoľnej
goniometrickej funkcie. Pomocou kalkulačky môžeme nakresliť aj graf funkcie závislej na parametroch. Tieto
parametre môžeme určiť ako meniteľné číselné hodnoty ako to je v Cabri výkrese Graf 1.
Graf 1
Parametre bolo možné zadať aj ako dĺžky úsečiek či súradnice bodov ktoré môžeme meniť pohybom myši,
ako je to vo výkrese Graf 2.
Graf 2
Nepripomína vám posúvanie parametrov vo výkrese Graf 2 niečo ako prácu s mixážnym pultom?
Úlohy
-
4.Koľkokrát sa budú hodinové ručičky v čase od $0$ hodín po $12$ hodín prekrývať? Použite riešenie 1. úlohy a uveďte všetky časy, kedy sa tak stane.
-
V operácii sčitovania bodov na kružnici má rovnica $\bf{n \cdot X = A}$ práve $n$ riešení. Aký obrazec tvoria tieto riešenia ?
-
Na obrázkoch v ukážkach „kotúľania a namotávania sú nakreslené krivky, ktoré vznikajú pohybom daných bodov. Skúste nájsť ich matematické vyjadrenie.
-
Vyjadrite s presnosťou na 6 desatinných miest $\bf{\cos 0.5}$.
Poznámka o riešení goniometrických rovníc.
Svoj názor na riešenie rovníc všetkých druhov sme vyjadrili v Poznámke 5. v kapitole III.1 Riešenie rovníc. Môžeme iba pridať jednu významnú metódu riešenia rovníc: „Pri riešení rovníc sa netreba držať žiadnej metódy“.
Príklad 5.
Vyriešte rovnicu: $\bf{tg x = tg(x + 10^\circ) \cdot tg(x+20^\circ)\cdot tg(x+30^\circ) \qquad (^4)} $
Riešenie.
Rovnicu „vynulujeme“ a nahradíme stupne radiánovou mierou: $$\bf{tg\bigg(x + \frac{\pi}{18}\bigg) \cdot tg\bigg(x+\frac{\pi}{9}\bigg) \cdot tg\bigg(x+\frac{\pi}{6}\bigg)-tgx = 0}$$
Nakreslíme si graf funkcie ľavej strany v DeadLine:
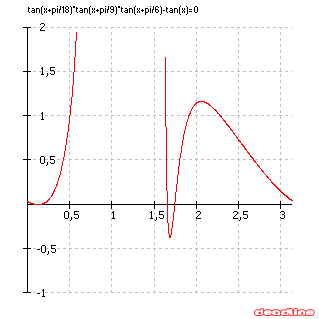
Funkcia je zrejme periodická s dĺžkou periódy $\pi$.
Otvorte si G19.
Príklad 6.
Vyriešte rovnicu $\bf{(\sin x)^2 = \sin(x^2), \; x \in \langle 0; \pi \rangle}$
Riešenie.
Korene by sme našli podobným spôsobom ako v predošlom príklade. Najprv z celkového pohľadu na graf funkcie $\bf{y = (\sin x)^2 - \sin(x^2), \; x \in \langle 0; \pi \rangle}$ by sme odhadli všetky (štyri) korene a potom by ich získali použitím ponuky „Find roots“ s presnosťou na 8 desatinných miest.
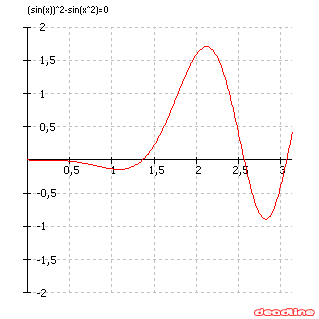
Situácia by sa však zmenila, keby bol oborom premennej väčší interval, napr. $\bf{x \in \langle 0 ; 4\pi \rangle}$. Tu by nás pohľad na graf v danom rozsahu premennej asi nepríjemne prekvapil:
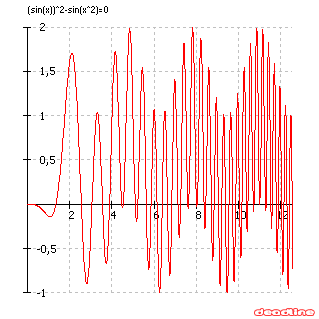
Nami doteraz ponúkaný spôsob riešenia by bol prinajmenšom zdĺhavý.
Otvorte si G20, skúste zmeniť hranice zobrazenej oblasti a zistíte, že akákoľvek výpočtová technika má
svoje hranice, za ktoré sa môže dostať len mysliaci človek.
G20.
Poznámka.
Podobné problémy, aké sme mali s funkciou $\bf{y = (\sin x)^2 - \sin(x^2)}$ pre veľké hodnoty premennej, by
vznikli s funkciou $\bf{y = \sin(\frac{1}{x})}$ v blízkosti nuly. Otvorte si G21 a presvedčte sa o tom aká
bude márna Vaša snaha sledovať priebeh tejto funkcie v blízkosti nuly.
Otvorte si G21.