Goniometrické funkcie
Predpokladám, že čitateľ postrehol, že sčitovanie bodov na kružnici je vlastne sčitovanie oblúkov kružnice, resp. skladanie otočení okolo stredu kružnice, čiže sčitovanie orientovaných uhlov.
Ak si napr. rovnicu (2) pretlmočíme do jazyka otáčaní, môžeme ju formulovať takto: „Aké otočenie (okolo bodu S) musíme vykonať trikrát po sebe, aby výsledkom bolo otočenie, ktoré otočí bod O do bodu B?“,
alebo v jazyku orientovaných uhlov: „Trojnásobok ktorého orientovaného uhla má základnú veľkosť $270^\circ$?“
Odpoveď znie: Také otočenia sú tri, lebo trikrát sa otočiť o uhol $90^\circ$ je to isté ako sa trikrát otočiť o uhol $210^\circ$, alebo sa trikrát otočiť o uhol $330^\circ$.
A tu sme pri koreni veci. Poslednej vete je ťažko uveriť. Predsa otočiť sa okolo vlastnej osi o $270^\circ$ je niečo iné než sa otočiť o $630^\circ$, či dokonca o $990^\circ$. Pletú sa nám dve veci:
-
reálna činnosť otáčania sa okolo vlastnej osi
-
matematický pojem otočenia okolo daného stredu o daný uhol
Uvedený príklad myslím si dostatočne ilustruje rozdiel medzi sčitovaním reálnych čísel a medzi sčitovaním orientovaných uhlov, či skladaním otočení okolo jedného stredu. Poskytuje aj dosť dôvodov na tvrdenie, že rovnica $\bf{n \cdot \alpha = \beta}$ má v množine orientovaných uhlov práve $\bf{n}$ riešení.
Už sme zrelí na to, aby sme vyriešili 1. úlohu:
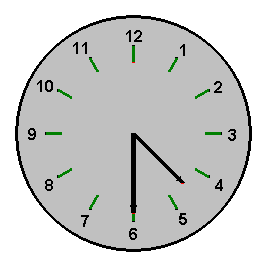
Za čas $\bf{t}$ prejde malá ručička uhol veľkosti $\bf{t \cdot 30^\circ}$ a veľká ručička uhol veľkosti $\bf{t \cdot 360^\circ}$. Preto budú hodinové ručičky v čase $\bf{t}$ zvierať uhol, ktorý bude rozdielom týchto uhlov, teda uhol, ktorého jednou veľkosťou bude $\bf{t \cdot 30^\circ - t \cdot 360^\circ = -t \cdot 330^\circ}$ napr. o pol piatej bude mať tento uhol veľkosť $\bf{-1485^\circ}$, čiže jeho základná veľkosť bude $\bf{– 1485^\circ + 5 \cdot 360^\circ = 315^\circ}$.
Príklad 4.
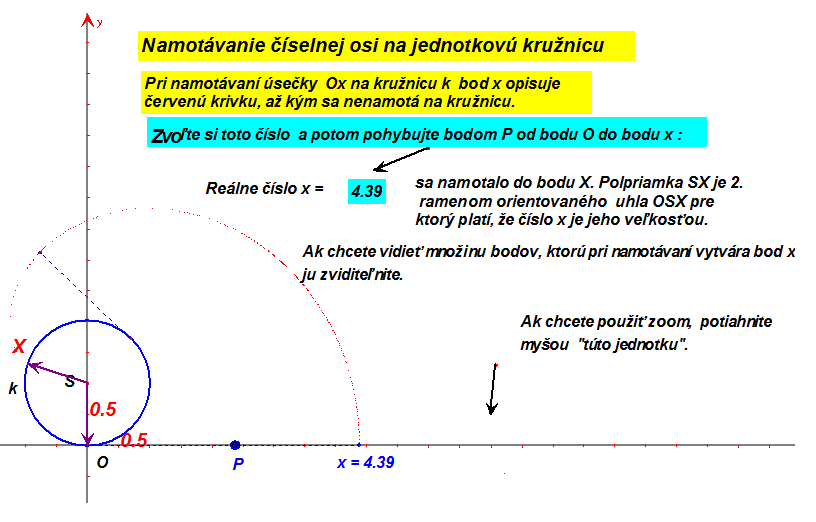
V príklade 1. spomenuté kotúľanie kružnice po priamke z matematického hľadiska nie je zobrazením. Jeden bod kružnice zanechá nekonečne veľa odtlačkov. Ako by asi vyzeral opačný proces t. j. „namotávanie“ číselnej osi na kružnicu, vidíme na nasledujúcom obrázku, ktorý si môžete pozrieť v živej podobe ako Cabri výkres namotávanie.