Goniometrické funkcie
Vlastnosti funkcií sínus a kosínus.
Z faktu, že bod $\bf{[\cos x ; \sin x]}$ je bodom jednotkovej kružnice, vyplýva ich prvá vlastnosť: $$\bf{\forall x \in R: \cos^2x + sin^2x = 1 \qquad(^3)}$$
Užitočnú informáciu môže dať pohľad na dva nasledujúce obrázky. Na oboch obrázkoch je zobrazený bod jednotkovej kružnice, ktorého súradnice sú $\bf{[a; b]}$, do ktorého sa namotá reálne číslo $\bf{\alpha}$ a jeho obrazy v súmernostiach podľa jednotlivých súradnicových osí aj podľa osí kvadrantov. V prvom obrázku sú body označené svojimi súradnicami a v druhom sme vyznačili, ktoré reálne čísla sa do nich namotali:
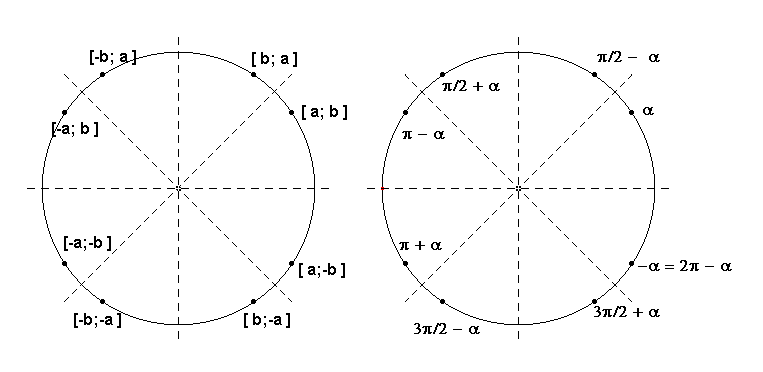
Ak teraz porovnáme oba obrázky a uvedomíme si, že $\bf{a = \cos \alpha, \; b = \sin \alpha}$ dostaneme týchto sedem dvojíc identít: \begin{array}{ll} \bf{\cos(\pi / 2 - x) = \sin x} & \bf{\sin(\pi / 2 - x) = \cos x}\\ \bf{\cos(\pi / 2 + x) = - \sin x} & \bf{\sin(\pi / 2 + x) = \cos x}\\ \bf{\cos(\pi - x) = - \cos x} & \bf{\sin(\pi - x) = \sin x}\\ \bf{\cos(\pi + x) = - \cos x} & \bf{\sin(\pi + x) = - \sin x}\\ \bf{\cos(3\pi / 2 - x) = - \sin x} & \bf{\sin(3\pi / 2 - x) = -\cos x}\\ \bf{\cos(3\pi / 2 + x) = \sin x} & \bf{\sin(3\pi / 2 + x) = -\cos x}\\ \bf{\cos(-x) = - \cos x} & \bf{\sin(- x) = -\sin x}\\ \end{array}
Najzaujímavejšie dvojice sú v prvom a v poslednom riadku.
Dobre si všimnite nasledujúci obrázok:
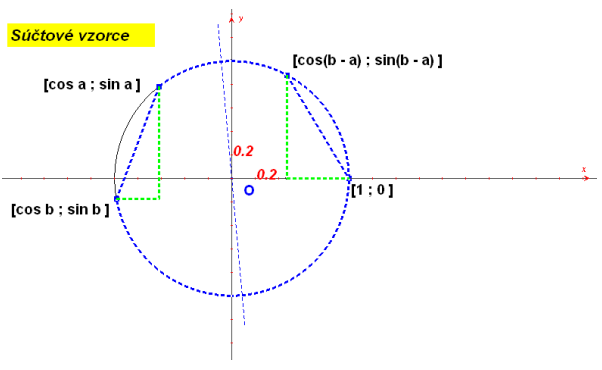
Z definície sčitovania bodov na kružnici vyplýva, že dĺžka úsečky spájajúcej body do ktorých sa namotajú čísla $\bf{a, b}$ je rovná dĺžke úsečky spájajúcej body, do ktorých sa namotajú čísla $\bf{0, b – a}$. Ak pomocou Pytagorovej vety vypočítame dĺžky týchto úsečiek a výsledky dáme do rovnosti postupne dostaneme: $$\bf{[\cos(b-a)-1]^2 + [\sin(b-a)-0]^2 = (\cos a - \cos b)^2 + (\sin a - \sin b)^2}$$ $$\bf{\bbox[yellow, 3px]{\cos(b-a) = (\cos a)(\cos b) + (\sin a)(\sin b)}}$$
Tomuto vzťahu a podobným vyjadreniam pre $\bf{\cos(a + b), \sin(a + b), \sin(a – b)}$ hovoríme súčtové vzorce. Tieto hrajú vážnu úlohu pri úpravách výrazov obsahujúcich goniometrické funkcie. Bez existencie výpočtovej techniky bola mimoriadne dôležitá schopnosť upravovať tzv. goniometrické výrazy. Bez toho bolo temer nemožné riešiť úlohy. V súčasnosti miesto tejto schopnosti sa stáva dôležitejšou schopnosť vedieť pri riešení problémov vhodne používať výpočtovú techniku.
Poznámka o funkciách tangens a kotangens
Funkcie tangens a kotangens sú definovaná (pre prípustné hodnoty premennej $\bf{x}$): $$\bf{tg x = \frac{\sin x}{\cos x} \qquad cotg x = \frac{\cos x}{\sin x} }$$